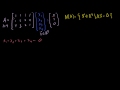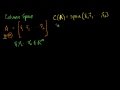Lec 38 - Null Space and Column Space Basis
Null Space and Column Space Basis Figuring out the null space and a basis of a column space for a matrix
Video is embedded from external source so embedding is not available.
Video is embedded from external source so download is not available.
Channels: Mathematics
Tags: Null Space and Column Space Basis
Uploaded by: khanlinearalgebr ( Send Message ) on 10-09-2012.
Duration: 25m 13s
Here is the next lecture for this course
Lec 36 - Null Space 3: Relation to Linear ...
11:35 | 2612 viewsLec 34 - Introduction to the Null Space o ...
10:23 | 2358 viewsLec 35 - Null Space 2: Calculating the nu ...
13:07 | 2336 viewsLec 37 - Column Space of a Matrix
10:40 | 2287 viewsLec 39 - Visualizing a Column Space as a ...
21:11 | 6552 viewsLec 41 - Dimension of the Null Space or N ...
13:59 | 2298 viewsLec 42 - Dimension of the Column Space or ...
12:48 | 2204 viewsThe Hubble Space Telescope
00:43 | 6589 viewsLanding of a Space Ship
00:26 | 8157 viewsSelf-Supporting Space Suit Makes It Hard ...
00:52 | 6547 viewsThe universe through the Hubble space tel ...
06:11 | 11177 viewsCERN AMS From CERN to Space!
05:27 | 5662 viewsCosmic Visions: New Space Science Missions
04:54 | 5799 viewsBefore Time and Space
03:28 | 7077 viewsRice University Physics and Astronomy: Sp ...
05:37 | 7342 viewsNo content is added to this lecture.
This video is a part of a lecture series from of khan