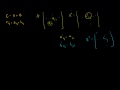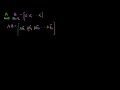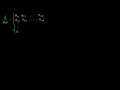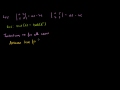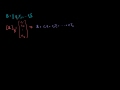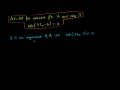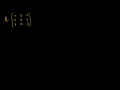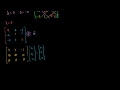Lec 94 - Linear Algebra: Transpose of a Matrix Product
Linear Algebra: Transpose of a Matrix Product Taking the transpose of the product of two matrices
Video is embedded from external source so embedding is not available.
Video is embedded from external source so download is not available.
Channels: Mathematics
Tags: Linear Algebra: Transpose of a Matrix Product
Uploaded by: khanlinearalgebr ( Send Message ) on 10-09-2012.
Duration: 8m 50s
Here is the next lecture for this course
Lec 64 - Linear Algebra: Matrix Product E ...
18:14 | 2276 viewsLec 92 - Linear Algebra: Transpose of a M ...
08:37 | 2618 viewsLec 93 - Linear Algebra: Determinant of ...
14:10 | 2636 viewsLec 96 - Linear Algebra: Transpose of a V ...
12:06 | 2259 viewsLec 27 - Linear Algebra: Cross Product In ...
15:47 | 2530 viewsLec 77 - Linear Algebra: Example of Findi ...
06:22 | 2748 viewsLec 73 - Linear Algebra: Matrix condition ...
19:59 | 2749 viewsLec 100 - Linear Algebra: Rank(A) = Rank( ...
11:13 | 2451 viewsLec 112 - Linear Algebra: Subspace Projec ...
13:04 | 2997 viewsLec 119 - Linear Algebra: Change of Basis ...
17:55 | 2968 viewsLec 136 - Linear Algebra: Example solving ...
05:39 | 2071 viewsLec 138 - Linear Algebra: Eigenvalues of ...
14:08 | 2356 viewsLec 139 - Linear Algebra: Eigenvectors a ...
15:34 | 2698 viewsLec 11 - MIT 18.06 Linear Algebra, Spring ...
45:56 | 3161 viewsLec 20 - MIT 18.06 Linear Algebra, Spring ...
51:01 | 2875 viewsNo content is added to this lecture.
This video is a part of a lecture series from of khan
Lecture list for this course
Lec 1 - Introduction to matrices
Lec 2 - Matrix multiplication (part 1)
Lec 3 - Matrix multiplication (part 2)
Lec 4 - Inverse Matrix (part 1)
Lec 5 - Inverting matrices (part 2)
Lec 6 - Inverting Matrices (part 3)
Lec 7 - Matrices to solve a system of equations
Lec 8 - Matrices to solve a vector combination problem
Lec 10 - 3- variable linear equations (part 1)
Lec 11 - Solving 3 Equations with 3 Unknowns
Lec 12 - Linear Algebra: Introduction to Vectors
Lec 13 - Linear Algebra: Vector Examples
Lec 14 - Linear Algebra: Parametric Representations of Lines
Lec 15 - Linear Combinations and Span
Lec 16 - Linear Algebra: Introduction to Linear Independence
Lec 17 - More on linear independence
Lec 18 - Span and Linear Independence Example
Lec 20 - Linear Algebra: Basis of a Subspace
Lec 21 - Vector Dot Product and Vector Length
Lec 22 - Proving Vector Dot Product Properties
Lec 23 - Proof of the Cauchy-Schwarz Inequality
Lec 24 - Linear Algebra: Vector Triangle Inequality
Lec 25 - Defining the angle between vectors
Lec 26 - Defining a plane in R3 with a point and normal vector
Lec 27 - Linear Algebra: Cross Product Introduction
Lec 28 - Proof: Relationship between cross product and sin of angle
Lec 29 - Dot and Cross Product Comparison/Intuition
Lec 30 - Matrices: Reduced Row Echelon Form 1
Lec 31 - Matrices: Reduced Row Echelon Form 2
Lec 32 - Matrices: Reduced Row Echelon Form 3
Lec 33 - Matrix Vector Products
Lec 34 - Introduction to the Null Space of a Matrix
Lec 35 - Null Space 2: Calculating the null space of a matrix
Lec 36 - Null Space 3: Relation to Linear Independence
Lec 37 - Column Space of a Matrix
Lec 38 - Null Space and Column Space Basis
Lec 39 - Visualizing a Column Space as a Plane in R3
Lec 40 - Proof: Any subspace basis has same number of elements
Lec 41 - Dimension of the Null Space or Nullity
Lec 42 - Dimension of the Column Space or Rank
Lec 43 - Showing relation between basis cols and pivot cols
Lec 44 - Showing that the candidate basis does span C(A)
Lec 45 - A more formal understanding of functions
Lec 46 - Vector Transformations
Lec 47 - Linear Transformations
Lec 48 - Matrix Vector Products as Linear Transformations
Lec 49 - Linear Transformations as Matrix Vector Products
Lec 50 - Image of a subset under a transformation
Lec 51 - im(T): Image of a Transformation
Lec 53 - Preimage and Kernel Example
Lec 54 - Sums and Scalar Multiples of Linear Transformations
Lec 55 - More on Matrix Addition and Scalar Multiplication
Lec 56 - Linear Transformation Examples: Scaling and Reflections
Lec 57 - Linear Transformation Examples: Rotations in R2
Lec 58 - Rotation in R3 around the X-axis
Lec 60 - Introduction to Projections
Lec 61 - Expressing a Projection on to a line as a Matrix Vector prod
Lec 62 - Compositions of Linear Transformations 1
Lec 63 - Compositions of Linear Transformations 2
Lec 64 - Linear Algebra: Matrix Product Examples
Lec 65 - Matrix Product Associativity
Lec 66 - Distributive Property of Matrix Products
Lec 67 - Linear Algebra: Introduction to the inverse of a function
Lec 68 - Proof: Invertibility implies a unique solution to f(x)=y
Lec 69 - Surjective (onto) and Injective (one-to-one) functions
Lec 70 - Relating invertibility to being onto and one-to-one
Lec 71 - Determining whether a transformation is onto
Lec 72 - Linear Algebra: Exploring the solution set of Ax=b
Lec 73 - Linear Algebra: Matrix condition for one-to-one trans
Lec 74 - Linear Algebra: Simplifying conditions for invertibility
Lec 75 - Linear Algebra: Showing that Inverses are Linear
Lec 76 - Linear Algebra: Deriving a method for determining inverses
Lec 77 - Linear Algebra: Example of Finding Matrix Inverse
Lec 78 - Linear Algebra: Formula for 2x2 inverse
Lec 79 - Linear Algebra: 3x3 Determinant
Lec 80 - Linear Algebra: nxn Determinant
Lec 81 - Linear Algebra: Determinants along other rows/cols
Lec 82 - Linear Algebra: Rule of Sarrus of Determinants
Lec 83 - Linear Algebra: Determinant when row multiplied by scalar
Lec 84 - Linear Algebra: (correction) scalar muliplication of row
Lec 85 - Linear Algebra: Determinant when row is added
Lec 86 - Linear Algebra: Duplicate Row Determinant
Lec 87 - Linear Algebra: Determinant after row operations
Lec 88 - Linear Algebra: Upper Triangular Determinant
Lec 89 - Linear Algebra: Simpler 4x4 determinant
Lec 90 - Linear Algebra: Determinant and area of a parallelogram
Lec 91 - Linear Algebra: Determinant as Scaling Factor
Lec 92 - Linear Algebra: Transpose of a Matrix
Lec 93 - Linear Algebra: Determinant of Transpose
Lec 95 - Linear Algebra: Transposes of sums and inverses
Lec 96 - Linear Algebra: Transpose of a Vector
Lec 97 - Linear Algebra: Rowspace and Left Nullspace
Lec 98 - Lin Alg: Visualizations of Left Nullspace and Rowspace
Lec 99 - Linear Algebra: Orthogonal Complements
Lec 100 - Linear Algebra: Rank(A) = Rank(transpose of A)
Lec 101 - Linear Algebra: dim(V) + dim(orthogonoal complelent of V)=n