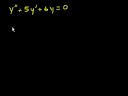A Particular Solutions Inhomogeneous 2nd Order...

A Particular Solutions Inhomogeneous 2nd Order ODE Formula

2414 views | 5m 42s

Help us improve our scientific videos to generate more reliable content. Please edit this video content so others will reach and understand it more easily.

Suggested Title:

Suggested Description:

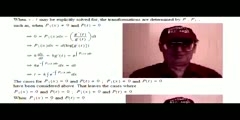
A Particular Solutions Formula For 
Inhomogeneous Second Order 
Linear Ordinary Differential Equations
    
      ©   2011  Claude Michael Cassano/nFinding a particular solutions to a linear inhomogeneous ordinary differential equation has always been a process of determining homogeneous solutions, and then adding any particular solution of the inhomogeneous equation. The well-known methods of undetermined coefficients and
variation of parameters have long been the standard in determining this particular solution. The former has sometimes been considered 'ad-hoc', and both can be intricate. A relatively simple formuila has been found which allows the particular solution to be written and evaluated immediately. 
           Corollary II.2 manifests the particular solution formula for second order
linear inhomogeneous ordinary diffrential equations. It shows that beyond equations
with constant coefficients, that particular solutions can be quite complicated and
demanding. Indeed, the method of undetermined coefficients is useless in more
demanding problems, and, although using the Wronskian method can be applied,
my Corollary II.2 formula requires only one of the homogeneous solutions be
determined - and is far more compactly and elegantly written. 
For second order ODEs these make the methods of undetermined coefficients and variation of parameters obsolete.
    
The proofs in more detail may be found in my book available on Kindle in digital format at amazon.com, and links to all my books may be found at:  /nhttps://sites.google.com/site/themathematicalnatureofreality//nhttps://sites.google.com/site/themathematicalnatureofreality/config/pagetemplates/books
... 
My 3rd & 4th order formulas are on video, now, and my arbitrary order book is available on kindle, now, too.

Suggested Keywords:

Close This Panel