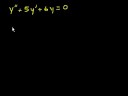2nd Order LODE Particular Solution Formula Advanced Examples
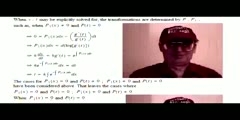
Second Order LODE Particular Solution Formula Advanced Examples/n Particular solution examples for Ordinary differential equations are traditionally restricted to constant coefficients equations. Further demonstration of the power of the formula at an elementary level may be made via application on non-constant coefficient LODEs. Consider the second order Cauchy-Euler LODE, as shown, here: y" + (2/x)y' + (1/(4x^2))y = W Go to Wolfrom Alpha website: http://www.wolframalpha.com/ for several verifications, including: y" + (A/x)y' + (((A-1)/2)^2)/(x^2)y = = x^(-B)/log(x) /n As always: All my books are available on Kindle in digital format and some in print at amazon.com. I appreciate the support you show by viewing my videos, but note that they are mostly merely summaries of my books. For a more complete picture of some of my results, obtaining my books would be a benefit to each of you, and an inexpensive further gesture and statement of support for me. I’ve set the price on both the printed version and the Kindle version low enough for anyone’s expendable budget. /n Links to all my books may be found at the following websites:/n https://sites.google.com/site/themathematicalnatureofreality//n https://sites.google.com/site/themathematicalnatureofreality/config/pagetemplates/books/nI am placing a donation button at the links in case you’d rather support in that way.
Channels: Mathematics
Tags: math ODE inhomogeneous differential equation particular solution
Uploaded by: cloudmichael ( Send Message ) on 05-07-2012.
Duration: 9m 24s