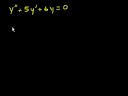Solving 2nd Order Linear ODEs - The Easy Way - DnaTube.com

3064 views

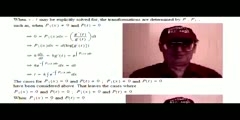
Solving 2nd Order Linear Ordinary Differential Equations - The Easy Way The exactly solvable 2nd order linear homogeneous ODEs: constant coefficients, Cauchy-Euler, and many more, may be addressed by a single simple technique reducing the ODE problem to a high school algebra problem. All the standard exactly solvable linear second order ordinary differential equations are special cases of the above theorem under the simple case: s=aP+b , (a,b constants). The elementary exactly solvable linear second order ordinary differential equations of the form: y′′+Py′+Qy=0 are Q=0 , Q=P′ , constant coefficients, and Cauchy-Euler. Clearly, the first case is given by: a=b=0. The second case is given by: s=-P. The third case is given by: P=A (A constant). The Cauchy-Euler case is given by: P=(A/x) (A constant), with b=0 In fact, a special case of the Bessel differential equation is satisfied with: a=-(1/2) (P=(1/x)). /nVisit my author page on amazon.com to find my books available on Kindle in digital and some in print at the website, here: /n http://www.amazon.com/Claude-Michael-Cassano/e/B008MD6CVS/ref=ntt_athr_dp_pel_1 Visit: http://www.barnesandnoble.com/s/claude-michael-cassano?keyword=claude+michael+ cassano&store=allproducts /nfor my books available on NOOK and some in print at barnes & noble.