Scientific Video Site

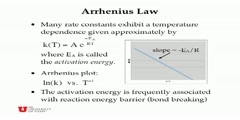
Description (Edit): Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 34/nTopics covered: /nKinetics (cont.)/nInstructor: /nProf. Catherine Drennan/nTranscript - Lecture 34/nAll right./nLet's continue then on this unit of kinetics. Today we are going to talk about temperature and we are going to talk about collisions and we are going to talk about activation energies and activated complexes./nAnd we are still in Chapter 13 in your book. When we started this unit on kinetics, we listed a bunch of things that can affect a rate of a reaction. And let's just review what we have talked about and what we have left to talk about./nWe talked about mechanisms of reactions. One step, two steps, fast steps, slow steps. That can affect the rate of the reaction. We talked about concentration of material. We talked about nature of material./nWe talked about first order and second order integrated rate laws. Today we are going to talk about temperature, then Monday we are going to talk about the use of catalysts, and then Wednesday again is a review./nWe are right at the bottom of our list here of things affecting rates of reaction. The affect of temperature. If you are in the gas-phase, it is sort of the qualitative observation that if you increase the temperature the rate increases./nYou've probably sort of thought about this, that if you want to make something go faster you add some heat. Today we are going to talk about quantitative affects and how you can actually calculate a change in rate constant if the temperature of the reaction is changed./nHere we go back to 1889. That is when Arrhenius plotted rate constants versus temperature. And he was looking to get a straight line. He found that if he used the natural log of the rate constants and plotted that against inverse temperature, he got a straight line./nHere is what one of those plots look like. The rate constants are varying exponentially with inverse temperature. On one axis, we have the natural log of the rate constant K. On the other axis, we have one over temperature./nAnd so this is the equation that is being plotted. Again, we have natural log of K on one axis. That is rate constant. The other axis is one over temperature. And so if this is one over temperature on this axis then the slope of the line is minus Ea, activation energy over R, which is the gas constant./nUp here, activation energy E sub a and R, our gas constant. And the intercept of the line then is the natural log of capital A. And capital A has several different names. You will see it listed in different books as different things./nI think our book usually refers to it as factor A, or the pre-exponential factor. And it would have the same units as K. If one plots natural log of rate constants over one temperature, one could determine the activation energy for a reaction or the factor A for a particular reaction./nThese quantities, factor A, and activation energy are dependent on the reaction being studied. There will be a particular measured value for one particular reaction. Let's think a little bit more about what these quantities are./nFactor A, is it temperature dependent? No, it is not temperature dependent. So what is it? Well, if we look over here, the natural log of A is going to equal the natural log of K at zero over here./nAnd that means when one over T is approximately zero. At what kinds of temperatures would one over T be approximately zero? Really, really big. Factor A is the rate constant for that reaction at some infinitely huge temperature./nThat is the maximum value that you could get for that rate constant. At really, really huge temperature that is what it is. It is not temperature dependent. It is a quantity that is the sort of maximum rate constant at the biggest temperature that you can think of./nThat is what factor A is. What about activation energy? Is that going to be temperature dependent? No, it won't be temperature dependent either. You can calculate it. It is the slope of the line./nSo you can get it out of plotting these values, but it is going to depend on the reaction being studied, not the particular temperature. And this is going to be important in a few minutes because we are going to be talking about the effects of rate constants on different temperatures and looking at equations and doing some calculations./nOK. We can rewrite this equation in a couple of different ways. You will see that equation for the straight line that Arrhenius came up with. It is called the Arrhenius equation. And it can be written basically just reversing these two terms, I guess because it looks better that way./nI am not really sure why you cannot just keep it like that, but you will see it this way. And you will also see it rewritten this way. Instead of natural log of K, you would see it as solved for K./nHere the rate constant is equal to A, which is this factor A. This rate constant at infinity huge temperatures times E to the minus Ea, the activation energy over RT. So you will also see this equation this way./nIt is a way of figuring out if you know the activation energy and you know factor A, you can calculate rate constants at a particular temperature. It is not only gases that behave in this way, that exhibit this Arrhenius behavior./nAnd you can apply these equations to other systems. And let's just look at one other example of something that behaves with Arrhenius behavior. What is that? Crickets. How many of you have heard crickets in the wild? Almost everybody./nI spent some years as a summer camp counselor, and we always had kids coming to the country from the city. And there would be crickets and bull frogs. And these poor kids that grew up right outside a hospital where all night long there would be ambulances going by and traffic and helicopters and all sorts of things would sleep fine at home, but then they would come to the country and couldn't sleep a wink because of all of this noise./nThe country is not as quiet as people think it is. Crickets will respond to temperature, and so they actually chirp faster when it is hotter. If you are out camping, you can count how many chirps there are in 14 seconds and add that to 40 and get the temperature in Fahrenheit./nHas anyone actually tried this? Did it work? You think so. Did you have a control of a thermometer with you? No. It probably works better if you don't actually have the control, but it should theoretically work if you can do a good job counting./nThat is an example of a non-gas exhibiting this behavior. All right. Let's talk more about the activation energy. We are going to talk a lot about activation energy today. Activation energy Ea. If you have two molecules coming together and colliding, sometimes they will form products and sometimes they will just fall away back into reactants./nNot every collision will result in product. Why is that? Only the collisions that have the right amount of energy can go on and form products. Really, what activation energy is, is some critical amount of energy that is required to go on and result in a reaction./nOnly the molecules with that critical energy, when they come together they will go onto product. Other molecules will come together, and they will just fall apart because they won't be able to overcome this activation energy barrier./nLet's look at the affect of temperature on the molecules that have critical amounts of energy. If we plot then fraction of molecules versus kinetic energy. And we can look at molecules that have a low temperature, or molecules at low temperature./nThere are some molecules at low temperature and we can look at some fractions of molecules at higher temperature, and then consider the critical energy needed to react. The activation energy. Molecules with that amount of energy or more will be able to react./nAnd, if you look at the fraction of molecules then that would have that energy, at higher temperatures more molecules have that critical amount of energy. And at lower temperature fewer molecules have that critical amount of energy./nSo temperature makes a difference. At higher temperature, more things will be able to react. That is what gets into this observation that reactions occur faster at higher temperature. More molecules have the critical energy needed to react when they are at higher temperature./nAt lower temperature it is more difficult. Fewer fractions of those molecules have that critical energy, can overcome an activation energy barrier. Let's look at an example now of if you know what the activation energy barrier is, figuring out different rate constants at different temperatures, how temperature is affecting the rate of the reaction./nThe example that we will look at is the hydrolysis of sucrose. And this is part of the digestive process. And digestion is a good thing. Let's look at this particular reaction. We are given an activation energy./nSomeone has measured the activation energy for the hydrolysis of sucrose, 108 kilojoules per mole. And someone has measured an observed rate, a K-obs of 1.0 times 10 to the minus 3 per molar per second at body temperature./nNow you are asked to figure out what would the observed rate constant be if you lowered that temperature, if you lowered it by 2 degrees to 35 degrees? You could right two different expressions. You can use Arrhenius equation and write two different expressions./nOver here we have the natural log of k1, the rate constant at one time, and t1 at that temperature. So, the rate constant at temperature one. That would be equal to the natural log of factor A. Again, that is not temperature dependent./nMinus Ea, the activation energy. And then it is over RT. And we write the same expression for a second temperature and a second rate constant. Now we can combine these two expressions and come up with one equation./nIf we subtract, we have natural log of the rate constant two minus the natural log of rate constant one. And that can also be expressed in terms of natural log of k2 over k1. And here we can pull out the temperature terms./nBoth of these have the same expression, minus Ea over R, the rate constant. And now we have the two temperatures. This expression is telling us how the rate constants are going to change with temperature for a particular activation energy./nWhat does this equation look like? It should look familiar to you. Something that we talked about before. What was that equation called? Van Hoff equation. And instead of rate constants we had what? Instead of rate constants there were? Equilibrium constants./nAnd instead of Ea we had what? What tells us about how equilibrium constants changes with temperature? If you have a reaction and you heat up the reaction, how do you know which direction it shifts? What is our predictive tool? Delta H, right./nThis equation is similar to one we saw before. Here we are comparing how rate constants change with temperature. And a predictive tool is the size, the magnitude of the activation energy. Before we were talking about how rate constants change with temperature./nAnd the predictive tool there was delta H. In case you need a review of this, we will review this actually at the end of the class because this is very exciting. At the end of the class we come back to Le Châteier's principle./nAnd we can explain Le Ch‚letier's principle in terms of temperature in a different way than we did when we started the course, because now we can think about it in terms of activation energies and rate constants./nWe will see that van Hoff equation again. For the moment now, we are just considering how rate constants are changing with temperature. We can plug in our values. The initial observed rate for the reaction at 37 degrees, and we have k2 that we are going to solve for./nWe were given the activation energy. And we know the gas constant and we were given the two temperatures. The only tricky thing here is to remember to get your units to cancel out. Often activation energies are given in kilojoules, whereas your gas constant is in joules./nThe temperatures here were given in Celsius, but if you are using the gas constant you are going to need to convert them to Kelvin for your units to cancel. The only thing tricky about this is to make sure that your units are going to cancel./nAnd so we can solve this for k2. And k2 comes out to be 7.6 times 10 to the minus 4 per molar per second. It would be the same units as k1, and that is quite a bit slower. We only changed our temperature by 2 degrees and yet the rate is quite a bit slower./nThe body temperature is the reactions, the enzymes in our bodies, and how much they need to work, how well they need to work is really optimized for the temperature of our particular body. If your body temperature drops quite a bit or if your body temperature goes up quite a bit, that is not good for the overall working of the human body./nJust some advice for a day like today. It is best to keep your body temperature at normal body temperature if you are spending a lot of time outside. Wear a hat, wear a scarf, wear gloves, wear real shoes, not sort of flip-flop type things, and you should be able to continue your hydrolyze your sucrose and digest./nYou have to start worrying about what clothes you are wearing this time of year in Boston, for those of you who are from warmer climates. All right. If we look at this equation again, we will see that if this term is large, if you have a large activation energy, if you have a large critical energy needed for that reaction to go then that reaction will be very sensitive to changes in temperature, i.e., if this is a big number then you are going to see a big difference between k1 and k2./nThis will tell you a lot about the reaction. And we will come back to this idea in a little bit. All right. Let's consider the reaction coordinate and activated complexes. There is this critical collision energy, this activation energy that is needed for these molecules to actually react./nWhy does this happen? Well, as two molecules may come toward each other, they may not be able to react if they don't have that energy. Well, why do they need energy? Well, they may need to sort of rearrange./nA bond may be broken. An atom may fall to the ground. New reactions are occurring. There is energy needed to get your desired product. They have to distort. The bonds need to distort, and that requires energy./nThe result is that usually that, before you go on to your product, so say this is one of your products, you need to usually form some kind of intermediate state, some kind of activated complex or transition state./nAnd that transition state can either go on to products or fall back to reactants. And only those molecules wit this energy can do this reaction, can overcome this barrier and go on to form products./nAnd I will show you a little movie of two molecules coming together. They are going to circle each other and figure out if they have the critical energy to react, and when they have that critical energy you will know it, and go onto product./nLet's just take a look at this reaction. Here comes molecule in red and in blue. They are checking each other out. They had enough energy and they went on and formed product. But only those molecules with that energy can go and form the product./nAll right. Let's draw a reaction coordinate now and look at these activation energy barriers and these transition complexes. All right. A reaction coordinate diagram has potential energy on one side./nAnd has the reaction coordinate on the other axis. And that just means the direction of the reaction. A reaction will start with reactants with a particular energy. In this case, we are going to look at NO2 plus CO./nWe have two reactants at a particular energy. And then these will react. They will need to form some kind of activated complex up here. Say, there are bonds distorting and new bonds forming. There is some kind of intermediate state, some kind of activated complex or transition state./nThere will be energy associated with getting up here. If they have the critical energy to react, they will go on then to products. And our products here are NO plus CO2. And these are our products./nAnd so that is what the reaction coordinate will look like. If they didn't have enough energy, it would just come back down here. This barrier up here is the activation energy for the forward reaction and this over here is the activation energy for the reverse reaction./nAnd, overall, you have a delta E for the system. So, the difference between the energy of the reactants and the products. Delta E is going to equal the activation energy for the forward reaction minus the activation energy for the reverse reaction./nAnd we can put some numbers on this. For the forward reaction it is 132 kilojoules per mole, for the reverse reaction we have 358 kilojoules per mole, and our overall delta E value is going to be minus 226 kilojoules per mole./nMinus 226 kilojoules per mole is going to be equal to the 132 kilojoules per mole minus the 358 kilojoules per mole. These are all going to add up. And that is one of the equations on your equation sheet that you need to know for the final that won't be provided./nBut it makes rational sense that these should all add up together. All right. How does this relate? Delta E, what is this delta E? Well, this is a quantity that can be measured. It is a thermodynamic quantity./nIt can come from calorimetry experiments. And it is related to a friend of ours, delta H. If you recall, delta H equals delta E plus the change in PV. And I think this was Lecture 17 from Professor Ceyer's notes when she started talking about thermodynamics./nAnd so most of the time, these are pretty similar to each other. For gases, there is a little bit of a difference. This term exists. You might have like a 1% to 2% difference, but is more or less the same./nIf it helps you to think about this as more or less the same as the delta H, that can be useful for you. They are very similar quantities there. OK. Again, there is a barrier. And for this reaction there is a smaller barrier going in the forward direction, the smaller activation energy, and a much bigger barrier for the reverse direction of this reaction./nIf we think about activation energy barriers, every reaction is going to have some activation energy barrier, just like most things we do in life have some activation energy barrier. For me, writing papers or writing grants, there is a very large activation energy barrier to get started./nThe getting started part, and it is usually kind of more like this direction. This kind of size activation energy barrier. Once I manage to kind of get up over the hump, really get started then it becomes much easier and I can really get going with this./nI imagine that if I recall back to studying for final exams, going back over the old material that you already covered and reviewing that there is a sizeable activation energy barrier to pulling out those first set of notes and pulling out Exam 1./nAnd looking at the things you got wrong and going back over it has an activation energy barrier. And what we are going to talk about on Monday a little bit are some tricks to get over those activation energy barriers./nCatalysts can lower the activation energy barrier. And, for most of us, an enormous level of stress can also help us get over that activation energy barrier. Your professor, for example, mentioning the final exam every day before class starts can be a little help getting over that activation energy barrier to start reviewing material./nThis kind of plot, you should feel like you should bond with this idea of activation energy barriers. You should understand the deepest level about these barriers that these molecules need to overcome./nAll right. Let's look at the affect of temperature on whether molecules can make it over those activation energy barriers. Again, for an elementary reaction there is always a barrier. Sometimes it is smaller, sometimes it is larger, but there is always a barrier to that./nThere is always a positive Ea here. OK. What happens if you increase temperature? If you increase temperature, it should increase the rate because of this down here. You increase temperature, more molecules will have the energy required to make it over that barrier./nFor an elementary reaction, increasing temperature will increase the rate. It will get over the barrier. For an overall reaction, for a more complicated reaction that has multiple steps, it is not necessarily clear that temperature is going to have this affect./nAnd let's consider why this is true. Let's look at the same reaction we looked at with mechanisms last time and figure out what all the K observed terms are. Are there small rate constants? Are there equilibrium constants? What does K-obs really mean? And then we can think about how temperature would affect those values./nHere we have a reaction with the fast reversible step followed by another step that is slow. We can say that the rate of product formation, our product here is NO2, is going to be equal to two because two were formed./nK2, this rate constant, times this intermediate here times the concentration of oxygen. That is just this last step. This slow step rate of formation of product. But this is an intermediate so we are not done./nWe have to get rid of this intermediate. And here we can do it fairly efficiently because we have a fast reversible step followed by a slow step. We can approximate that this step is in equilibrium./nAnd, if we approximate that, then we can solve for this intermediate in terms of an equilibrium expression. Again, the first step fast and reversible, the second step slow. This is pretty much in equilibrium./nNot much of this intermediate is being siphoned off to products. We can solve by setting up an equilibrium expression. Here is the equilibrium expression. Equilibrium constant for Step 1 equals rate constant for the forward reaction over rate constant for the reverse reaction equals products over reactants./nThere are two reactants, 2NO, so it is NO squared. And we can solve for the concentration of the intermediate then, which would be k1 times NO squared. Now we can substitute that in the overall expression, and we have this expression here./nNow our K-ops is going to be equal to this 2k2 and big k1. This is what we need to consider, how that is affected by temperature. Little k2 is an elementary rate constant. For an elementary reaction, increasing temperature will always increase rate./nWe know how this affected. And here is our expression that we looked at before. Now, what about the equilibrium constant? How do you know what is going to happen with an equilibrium constant, if it will get bigger or smaller with temperature? What is the equation that relates equilibrium constants and temperature? Van Hoff, right./nIt depends on delta H. It depends on whether the reaction is endothermic or exothermic. And here is that expression. You can see these are really very similar expressions. Here we have the equilibrium constants./nDelta H is our predictive tool. Whether that is endothermic or exothermic will depend on what direction it goes. It will depend on whether k1 is bigger than k2 or k2 is bigger than k1 with change in temperature./nAnd over here we have the expression that relates rate constants with temperature. And, in terms of sign, that is not an issue here because activation energy is always positive. There is always a barrier to overcome./nThat is always positive. Never a negative barrier. There is no sign change here, but there is an effective magnitude of that value as there is with this. So it is not so simple. If you have a multi-step reaction, it is not always so simple to predict the affect of temperature because it may be changing one thing in one way and something else in another way./nLet's consider this particular one here. Again, little K is always going to increase with temperature. The equilibrium constant, in this case, will decrease because it is an exothermic reaction. This particular reaction is exothermic./nIf we think about Le Châteier or we think about the van Hoff equation, we say if it an exothermic reaction, increasing the temperature will decrease the K because you are going to shift the reaction in the endothermic reaction to use up the heat./nThe magnitude of the increase or decrease will depend on the magnitude of the energy barrier and the magnitude of delta H. If we look at this particular example and you are told that the activation energy is a small number, it is not a very big activation energy barrier./nAnd you are also told then that delta H is a big number and it is a big negative number, what would that mean then? Well, if you look at this, if you have a small number for activation energy then there is not going to be a big difference between the Ks./nThe rate constant is only going to increase a little bit because this is a small number. On the other hand, if delta H is a big number, and you are told delta H is a big number, then the equilibrium constant should be very sensitive to changes in temperature./nYou should see a big difference in the equilibrium constants because this is a really big number. This particular reaction is an example where increasing the temperature can actually decrease the observed rate./nAnd the effect is because of the delta H. Again, a large activation energy means that the rate constant is very sensitive to changes in temperature, a large delta H means that the equilibrium constant is very sensitive to changes in temperature./nOur predictors are activation energy and also delta H in thinking about what might happen when the temperature of a reaction changes. And we mentioned that this is always going to increase, rate constant will always increase with temperature./nAnd you can easily remember this, that there is always a barrier. You don't get a great deal. There is always a barrier to overcome. And delta H can be positive or negative, so equilibrium constants can increase or decrease with temperature./nFor delta H, magnitude of delta H indicates the magnitude of the change. Sign of delta H indicates the direction of the change. And, if you forget that, you can just look at the equations and they will tell you the same thing./nNow we can come back to Le Châteier. We can explain those observations about how equilibrium constants changed. And how the reaction was affected, why you would shift in one direction versus another when you change the temperature./nAgain, Le Châteier says that a system that is at equilibrium, if you have the system at equilibrium and you apply a stress, the system will respond in such a way to minimize that stress. If you increased the temperature, the equilibrium should shift in the endothermic direction./nThat would be what the prediction would be from Le Châteier, because if you put in more heat the reaction wants to respond in a way to decrease the heat. And so it goes in the direction that absorbed heat, the endothermic direction./nThis is what we talked about before, but now we can think about this in a little bit of a different way in terms of these reaction coordinate diagrams. Let's look at an endothermic versus exothermic reaction./nHere we have an endothermic reaction. We have reactants here, we have a large activation energy in the forward direction, we have products up here and a smaller activation energy in the reverse direction./nFor this exothermic reaction, we have a smaller activation energy in the forward direction. And a much larger one in the reverse direction. Our equation here would then indicate you have an endothermic reaction, your delta E is positive, if you have a big number for the forward minus a small number for the reverse./nThat is going to give you a positive overall number. Whereas, in this case, if you have a small number here minus a much bigger number, you get a negative number for delta E or an exothermic reaction./nIf you are given information about the activation energy in the forward direction and in the reverse direction and ask if a reaction is endothermic or exothermic, you can figure that out using this equation./nNow let's think about temperature. If there is a small barrier, only a small barrier, most of your molecules can probably get over that small barrier. It's not that hard. But if there is a very large barrier, that is a problem./nTemperature helps with the big barriers. The small barrier, the molecules are going over anyway. The bigger barriers, they need extra help. They need the help of increased temperature. If we consider what happens, increasing temperature here, the big barrier is the forward direction./nIncreasing the temperature will make it easier to overcome this very large barrier. It makes very little difference here. The molecules are already doing fine getting over the small barrier, but here there is a big help./nWhat this does then is it shifts the equilibrium toward products. Increasing temperature for an endothermic reaction shifts toward products. That is what we learned before, but we had a different rationale for it last time./nNow let's consider this case. If you increase temperature, it is going to affect the reverse barrier more. That is the big barrier. This is where molecules are having a difficult time. They are getting over that barrier already, so in this case, when you have this exothermic reaction, adding temperature is going to shift toward reactants./nIt will shift it in the endothermic direction using up the heat. Again, this is what we saw before. But now we have a different explanation for why. Again, a large activation energy barrier means that the rate constants are very sensitive to temperature./nIt is highly affected. If it is big, it is large. It needs temperature for the molecules to get over. Increasing the temperature has a big affect. Now molecules can do it. They can get over. This is why a large barrier means that a reaction is sensitive to temperature./nBig activation energy, big difference. Small activation energy, not such a big difference./n< back to video index/nTopics covered: /nKinetics (cont.)/nInstructor: /nProf. Catherine Drennan/nTranscript: (HTML) (PDF) /nFree downloads: Video: iTunes U (MP4) Internet Archive (MP4) Internet Archive (RM)/nAudio: iTunes U (MP3) Internet Archive (MP3)/nFree streaming: VideoLectures.net /nResources: Lecture Notes (PDF) Syllabus/n /n /nTranscript - Lecture 34/nAll right./nLet's continue then on this unit of kinetics. Today we are going to talk about temperature and we are going to talk about collisions and we are going to talk about activation energies and activated complexes./nAnd we are still in Chapter 13 in your book. When we started this unit on kinetics, we listed a bunch of things that can affect a rate of a reaction. And let's just review what we have talked about and what we have left to talk about./nWe talked about mechanisms of reactions. One step, two steps, fast steps, slow steps. That can affect the rate of the reaction. We talked about concentration of material. We talked about nature of material./nWe talked about first order and second order integrated rate laws. Today we are going to talk about temperature, then Monday we are going to talk about the use of catalysts, and then Wednesday again is a review./nWe are right at the bottom of our list here of things affecting rates of reaction. The affect of temperature. If you are in the gas-phase, it is sort of the qualitative observation that if you increase the temperature the rate increases./nYou've probably sort of thought about this, that if you want to make something go faster you add some heat. Today we are going to talk about quantitative affects and how you can actually calculate a change in rate constant if the temperature of the reaction is changed./nHere we go back to 1889. That is when Arrhenius plotted rate constants versus temperature. And he was looking to get a straight line. He found that if he used the natural log of the rate constants and plotted that against inverse temperature, he got a straight line./nHere is what one of those plots look like. The rate constants are varying exponentially with inverse temperature. On one axis, we have the natural log of the rate constant K. On the other axis, we have one over temperature./nAnd so this is the equation that is being plotted. Again, we have natural log of K on one axis. That is rate constant. The other axis is one over temperature. And so if this is one over temperature on this axis then the slope of the line is minus Ea, activation energy over R, which is the gas constant./nUp here, activation energy E sub a and R, our gas constant. And the intercept of the line then is the natural log of capital A. And capital A has several different names. You will see it listed in different books as different things./nI think our book usually refers to it as factor A, or the pre-exponential factor. And it would have the same units as K. If one plots natural log of rate constants over one temperature, one could determine the activation energy for a reaction or the factor A for a particular reaction./nThese quantities, factor A, and activation energy are dependent on the reaction being studied. There will be a particular measured value for one particular reaction. Let's think a little bit more about what these quantities are./nFactor A, is it temperature dependent? No, it is not temperature dependent. So what is it? Well, if we look over here, the natural log of A is going to equal the natural log of K at zero over here./nAnd that means when one over T is approximately zero. At what kinds of temperatures would one over T be approximately zero? Really, really big. Factor A is the rate constant for that reaction at some infinitely huge temperature./nThat is the maximum value that you could get for that rate constant. At really, really huge temperature that is what it is. It is not temperature dependent. It is a quantity that is the sort of maximum rate constant at the biggest temperature that you can think of./nThat is what factor A is. What about activation energy? Is that going to be temperature dependent? No, it won't be temperature dependent either. You can calculate it. It is the slope of the line./nSo you can get it out of plotting these values, but it is going to depend on the reaction being studied, not the particular temperature. And this is going to be important in a few minutes because we are going to be talking about the effects of rate constants on different temperatures and looking at equations and doing some calculations./nOK. We can rewrite this equation in a couple of different ways. You will see that equation for the straight line that Arrhenius came up with. It is called the Arrhenius equation. And it can be written basically just reversing these two terms, I guess because it looks better that way./nI am not really sure why you cannot just keep it like that, but you will see it this way. And you will also see it rewritten this way. Instead of natural log of K, you would see it as solved for K./nHere the rate constant is equal to A, which is this factor A. This rate constant at infinity huge temperatures times E to the minus Ea, the activation energy over RT. So you will also see this equation this way./nIt is a way of figuring out if you know the activation energy and you know factor A, you can calculate rate constants at a particular temperature. It is not only gases that behave in this way, that exhibit this Arrhenius behavior./nAnd you can apply these equations to other systems. And let's just look at one other example of something that behaves with Arrhenius behavior. What is that? Crickets. How many of you have heard crickets in the wild? Almost everybody./nI spent some years as a summer camp counselor, and we always had kids coming to the country from the city. And there would be crickets and bull frogs. And these poor kids that grew up right outside a hospital where all night long there would be ambulances going by and traffic and helicopters and all sorts of things would sleep fine at home, but then they would come to the country and couldn't sleep a wink because of all of this noise./nThe country is not as quiet as people think it is. Crickets will respond to temperature, and so they actually chirp faster when it is hotter. If you are out camping, you can count how many chirps there are in 14 seconds and add that to 40 and get the temperature in Fahrenheit./nHas anyone actually tried this? Did it work? You think so. Did you have a control of a thermometer with you? No. It probably works better if you don't actually have the control, but it should theoretically work if you can do a good job counting./nThat is an example of a non-gas exhibiting this behavior. All right. Let's talk more about the activation energy. We are going to talk a lot about activation energy today. Activation energy Ea. If you have two molecules coming together and colliding, sometimes they will form products and sometimes they will just fall away back into reactants./nNot every collision will result in product. Why is that? Only the collisions that have the right amount of energy can go on and form products. Really, what activation energy is, is some critical amount of energy that is required to go on and result in a reaction./nOnly the molecules with that critical energy, when they come together they will go onto product. Other molecules will come together, and they will just fall apart because they won't be able to overcome this activation energy barrier./nLet's look at the affect of temperature on the molecules that have critical amounts of energy. If we plot then fraction of molecules versus kinetic energy. And we can look at molecules that have a low temperature, or molecules at low temperature./nThere are some molecules at low temperature and we can look at some fractions of molecules at higher temperature, and then consider the critical energy needed to react. The activation energy. Molecules with that amount of energy or more will be able to react./nAnd, if you look at the fraction of molecules then that would have that energy, at higher temperatures more molecules have that critical amount of energy. And at lower temperature fewer molecules have that critical amount of energy./nSo temperature makes a difference. At higher temperature, more things will be able to react. That is what gets into this observation that reactions occur faster at higher temperature. More molecules have the critical energy needed to react when they are at higher temperature./nAt lower temperature it is more difficult. Fewer fractions of those molecules have that critical energy, can overcome an activation energy barrier. Let's look at an example now of if you know what the activation energy barrier is, figuring out different rate constants at different temperatures, how temperature is affecting the rate of the reaction./nThe example that we will look at is the hydrolysis of sucrose. And this is part of the digestive process. And digestion is a good thing. Let's look at this particular reaction. We are given an activation energy./nSomeone has measured the activation energy for the hydrolysis of sucrose, 108 kilojoules per mole. And someone has measured an observed rate, a K-obs of 1.0 times 10 to the minus 3 per molar per second at body temperature./nNow you are asked to figure out what would the observed rate constant be if you lowered that temperature, if you lowered it by 2 degrees to 35 degrees? You could right two different expressions. You can use Arrhenius equation and write two different expressions./nOver here we have the natural log of k1, the rate constant at one time, and t1 at that temperature. So, the rate constant at temperature one. That would be equal to the natural log of factor A. Again, that is not temperature dependent./nMinus Ea, the activation energy. And then it is over RT. And we write the same expression for a second temperature and a second rate constant. Now we can combine these two expressions and come up with one equation./nIf we subtract, we have natural log of the rate constant two minus the natural log of rate constant one. And that can also be expressed in terms of natural log of k2 over k1. And here we can pull out the temperature terms./nBoth of these have the same expression, minus Ea over R, the rate constant. And now we have the two temperatures. This expression is telling us how the rate constants are going to change with temperature for a particular activation energy./nWhat does this equation look like? It should look familiar to you. Something that we talked about before. What was that equation called? Van Hoff equation. And instead of rate constants we had what? Instead of rate constants there were? Equilibrium constants./nAnd instead of Ea we had what? What tells us about how equilibrium constants changes with temperature? If you have a reaction and you heat up the reaction, how do you know which direction it shifts? What is our predictive tool? Delta H, right./nThis equation is similar to one we saw before. Here we are comparing how rate constants change with temperature. And a predictive tool is the size, the magnitude of the activation energy. Before we were talking about how rate constants change with temperature./nAnd the predictive tool there was delta H. In case you need a review of this, we will review this actually at the end of the class because this is very exciting. At the end of the class we come back to Le Châteier's principle./nAnd we can explain Le Ch‚letier's principle in terms of temperature in a different way than we did when we started the course, because now we can think about it in terms of activation energies and rate constants./nWe will see that van Hoff equation again. For the moment now, we are just considering how rate constants are changing with temperature. We can plug in our values. The initial observed rate for the reaction at 37 degrees, and we have k2 that we are going to solve for./nWe were given the activation energy. And we know the gas constant and we were given the two temperatures. The only tricky thing here is to remember to get your units to cancel out. Often activation energies are given in kilojoules, whereas your gas constant is in joules./nThe temperatures here were given in Celsius, but if you are using the gas constant you are going to need to convert them to Kelvin for your units to cancel. The only thing tricky about this is to make sure that your units are going to cancel./nAnd so we can solve this for k2. And k2 comes out to be 7.6 times 10 to the minus 4 per molar per second. It would be the same units as k1, and that is quite a bit slower. We only changed our temperature by 2 degrees and yet the rate is quite a bit slower./nThe body temperature is the reactions, the enzymes in our bodies, and how much they need to work, how well they need to work is really optimized for the temperature of our particular body. If your body temperature drops quite a bit or if your body temperature goes up quite a bit, that is not good for the overall working of the human body./nJust some advice for a day like today. It is best to keep your body temperature at normal body temperature if you are spending a lot of time outside. Wear a hat, wear a scarf, wear gloves, wear real shoes, not sort of flip-flop type things, and you should be able to continue your hydrolyze your sucrose and digest./nYou have to start worrying about what clothes you are wearing this time of year in Boston, for those of you who are from warmer climates. All right. If we look at this equation again, we will see that if this term is large, if you have a large activation energy, if you have a large critical energy needed for that reaction to go then that reaction will be very sensitive to changes in temperature, i.e., if this is a big number then you are going to see a big difference between k1 and k2./nThis will tell you a lot about the reaction. And we will come back to this idea in a little bit. All right. Let's consider the reaction coordinate and activated complexes. There is this critical collision energy, this activation energy that is needed for these molecules to actually react./nWhy does this happen? Well, as two molecules may come toward each other, they may not be able to react if they don't have that energy. Well, why do they need energy? Well, they may need to sort of rearrange./nA bond may be broken. An atom may fall to the ground. New reactions are occurring. There is energy needed to get your desired product. They have to distort. The bonds need to distort, and that requires energy./nThe result is that usually that, before you go on to your product, so say this is one of your products, you need to usually form some kind of intermediate state, some kind of activated complex or transition state./nAnd that transition state can either go on to products or fall back to reactants. And only those molecules wit this energy can do this reaction, can overcome this barrier and go on to form products./nAnd I will show you a little movie of two molecules coming together. They are going to circle each other and figure out if they have the critical energy to react, and when they have that critical energy you will know it, and go onto product./nLet's just take a look at this reaction. Here comes molecule in red and in blue. They are checking each other out. They had enough energy and they went on and formed product. But only those molecules with that energy can go and form the product./nAll right. Let's draw a reaction coordinate now and look at these activation energy barriers and these transition complexes. All right. A reaction coordinate diagram has potential energy on one side./nAnd has the reaction coordinate on the other axis. And that just means the direction of the reaction. A reaction will start with reactants with a particular energy. In this case, we are going to look at NO2 plus CO./nWe have two reactants at a particular energy. And then these will react. They will need to form some kind of activated complex up here. Say, there are bonds distorting and new bonds forming. There is some kind of intermediate state, some kind of activated complex or transition state./nThere will be energy associated with getting up here. If they have the critical energy to react, they will go on then to products. And our products here are NO plus CO2. And these are our products./nAnd so that is what the reaction coordinate will look like. If they didn't have enough energy, it would just come back down here. This barrier up here is the activation energy for the forward reaction and this over here is the activation energy for the reverse reaction./nAnd, overall, you have a delta E for the system. So, the difference between the energy of the reactants and the products. Delta E is going to equal the activation energy for the forward reaction minus the activation energy for the reverse reaction./nAnd we can put some numbers on this. For the forward reaction it is 132 kilojoules per mole, for the reverse reaction we have 358 kilojoules per mole, and our overall delta E value is going to be minus 226 kilojoules per mole./nMinus 226 kilojoules per mole is going to be equal to the 132 kilojoules per mole minus the 358 kilojoules per mole. These are all going to add up. And that is one of the equations on your equation sheet that you need to know for the final that won't be provided./nBut it makes rational sense that these should all add up together. All right. How does this relate? Delta E, what is this delta E? Well, this is a quantity that can be measured. It is a thermodynamic quantity./nIt can come from calorimetry experiments. And it is related to a friend of ours, delta H. If you recall, delta H equals delta E plus the change in PV. And I think this was Lecture 17 from Professor Ceyer's notes when she started talking about thermodynamics./nAnd so most of the time, these are pretty similar to each other. For gases, there is a little bit of a difference. This term exists. You might have like a 1% to 2% difference, but is more or less the same./nIf it helps you to think about this as more or less the same as the delta H, that can be useful for you. They are very similar quantities there. OK. Again, there is a barrier. And for this reaction there is a smaller barrier going in the forward direction, the smaller activation energy, and a much bigger barrier for the reverse direction of this reaction./nIf we think about activation energy barriers, every reaction is going to have some activation energy barrier, just like most things we do in life have some activation energy barrier. For me, writing papers or writing grants, there is a very large activation energy barrier to get started./nThe getting started part, and it is usually kind of more like this direction. This kind of size activation energy barrier. Once I manage to kind of get up over the hump, really get started then it becomes much easier and I can really get going with this./nI imagine that if I recall back to studying for final exams, going back over the old material that you already covered and reviewing that there is a sizeable activation energy barrier to pulling out those first set of notes and pulling out Exam 1./nAnd looking at the things you got wrong and going back over it has an activation energy barrier. And what we are going to talk about on Monday a little bit are some tricks to get over those activation energy barriers./nCatalysts can lower the activation energy barrier. And, for most of us, an enormous level of stress can also help us get over that activation energy barrier. Your professor, for example, mentioning the final exam every day before class starts can be a little help getting over that activation energy barrier to start reviewing material./nThis kind of plot, you should feel like you should bond with this idea of activation energy barriers. You should understand the deepest level about these barriers that these molecules need to overcome./nAll right. Let's look at the affect of temperature on whether molecules can make it over those activation energy barriers. Again, for an elementary reaction there is always a barrier. Sometimes it is smaller, sometimes it is larger, but there is always a barrier to that./nThere is always a positive Ea here. OK. What happens if you increase temperature? If you increase temperature, it should increase the rate because of this down here. You increase temperature, more molecules will have the energy required to make it over that barrier./nFor an elementary reaction, increasing temperature will increase the rate. It will get over the barrier. For an overall reaction, for a more complicated reaction that has multiple steps, it is not necessarily clear that temperature is going to have this affect./nAnd let's consider why this is true. Let's look at the same reaction we looked at with mechanisms last time and figure out what all the K observed terms are. Are there small rate constants? Are there equilibrium constants? What does K-obs really mean? And then we can think about how temperature would affect those values./nHere we have a reaction with the fast reversible step followed by another step that is slow. We can say that the rate of product formation, our product here is NO2, is going to be equal to two because two were formed./nK2, this rate constant, times this intermediate here times the concentration of oxygen. That is just this last step. This slow step rate of formation of product. But this is an intermediate so we are not done./nWe have to get rid of this intermediate. And here we can do it fairly efficiently because we have a fast reversible step followed by a slow step. We can approximate that this step is in equilibrium./nAnd, if we approximate that, then we can solve for this intermediate in terms of an equilibrium expression. Again, the first step fast and reversible, the second step slow. This is pretty much in equilibrium./nNot much of this intermediate is being siphoned off to products. We can solve by setting up an equilibrium expression. Here is the equilibrium expression. Equilibrium constant for Step 1 equals rate constant for the forward reaction over rate constant for the reverse reaction equals products over reactants./nThere are two reactants, 2NO, so it is NO squared. And we can solve for the concentration of the intermediate then, which would be k1 times NO squared. Now we can substitute that in the overall expression, and we have this expression here./nNow our K-ops is going to be equal to this 2k2 and big k1. This is what we need to consider, how that is affected by temperature. Little k2 is an elementary rate constant. For an elementary reaction, increasing temperature will always increase rate./nWe know how this affected. And here is our expression that we looked at before. Now, what about the equilibrium constant? How do you know what is going to happen with an equilibrium constant, if it will get bigger or smaller with temperature? What is the equation that relates equilibrium constants and temperature? Van Hoff, right./nIt depends on delta H. It depends on whether the reaction is endothermic or exothermic. And here is that expression. You can see these are really very similar expressions. Here we have the equilibrium constants./nDelta H is our predictive tool. Whether that is endothermic or exothermic will depend on what direction it goes. It will depend on whether k1 is bigger than k2 or k2 is bigger than k1 with change in temperature./nAnd over here we have the expression that relates rate constants with temperature. And, in terms of sign, that is not an issue here because activation energy is always positive. There is always a barrier to overcome./nThat is always positive. Never a negative barrier. There is no sign change here, but there is an effective magnitude of that value as there is with this. So it is not so simple. If you have a multi-step reaction, it is not always so simple to predict the affect of temperature because it may be changing one thing in one way and something else in another way./nLet's consider this particular one here. Again, little K is always going to increase with temperature. The equilibrium constant, in this case, will decrease because it is an exothermic reaction. This particular reaction is exothermic./nIf we think about Le Châteier or we think about the van Hoff equation, we say if it an exothermic reaction, increasing the temperature will decrease the K because you are going to shift the reaction in the endothermic reaction to use up the heat./nThe magnitude of the increase or decrease will depend on the magnitude of the energy barrier and the magnitude of delta H. If we look at this particular example and you are told that the activation energy is a small number, it is not a very big activation energy barrier./nAnd you are also told then that delta H is a big number and it is a big negative number, what would that mean then? Well, if you look at this, if you have a small number for activation energy then there is not going to be a big difference between the Ks./nThe rate constant is only going to increase a little bit because this is a small number. On the other hand, if delta H is a big number, and you are told delta H is a big number, then the equilibrium constant should be very sensitive to changes in temperature./nYou should see a big difference in the equilibrium constants because this is a really big number. This particular reaction is an example where increasing the temperature can actually decrease the observed rate./nAnd the effect is because of the delta H. Again, a large activation energy means that the rate constant is very sensitive to changes in temperature, a large delta H means that the equilibrium constant is very sensitive to changes in temperature./nOur predictors are activation energy and also delta H in thinking about what might happen when the temperature of a reaction changes. And we mentioned that this is always going to increase, rate constant will always increase with temperature./nAnd you can easily remember this, that there is always a barrier. You don't get a great deal. There is always a barrier to overcome. And delta H can be positive or negative, so equilibrium constants can increase or decrease with temperature./nFor delta H, magnitude of delta H indicates the magnitude of the change. Sign of delta H indicates the direction of the change. And, if you forget that, you can just look at the equations and they will tell you the same thing./nNow we can come back to Le Châteier. We can explain those observations about how equilibrium constants changed. And how the reaction was affected, why you would shift in one direction versus another when you change the temperature./nAgain, Le Châteier says that a system that is at equilibrium, if you have the system at equilibrium and you apply a stress, the system will respond in such a way to minimize that stress. If you increased the temperature, the equilibrium should shift in the endothermic direction./nThat would be what the prediction would be from Le Châteier, because if you put in more heat the reaction wants to respond in a way to decrease the heat. And so it goes in the direction that absorbed heat, the endothermic direction./nThis is what we talked about before, but now we can think about this in a little bit of a different way in terms of these reaction coordinate diagrams. Let's look at an endothermic versus exothermic reaction./nHere we have an endothermic reaction. We have reactants here, we have a large activation energy in the forward direction, we have products up here and a smaller activation energy in the reverse direction./nFor this exothermic reaction, we have a smaller activation energy in the forward direction. And a much larger one in the reverse direction. Our equation here would then indicate you have an endothermic reaction, your delta E is positive, if you have a big number for the forward minus a small number for the reverse./nThat is going to give you a positive overall number. Whereas, in this case, if you have a small number here minus a much bigger number, you get a negative number for delta E or an exothermic reaction./nIf you are given information about the activation energy in the forward direction and in the reverse direction and ask if a reaction is endothermic or exothermic, you can figure that out using this equation./nNow let's think about temperature. If there is a small barrier, only a small barrier, most of your molecules can probably get over that small barrier. It's not that hard. But if there is a very large barrier, that is a problem./nTemperature helps with the big barriers. The small barrier, the molecules are going over anyway. The bigger barriers, they need extra help. They need the help of increased temperature. If we consider what happens, increasing temperature here, the big barrier is the forward direction./nIncreasing the temperature will make it easier to overcome this very large barrier. It makes very little difference here. The molecules are already doing fine getting over the small barrier, but here there is a big help./nWhat this does then is it shifts the equilibrium toward products. Increasing temperature for an endothermic reaction shifts toward products. That is what we learned before, but we had a different rationale for it last time./nNow let's consider this case. If you increase temperature, it is going to affect the reverse barrier more. That is the big barrier. This is where molecules are having a difficult time. They are getting over that barrier already, so in this case, when you have this exothermic reaction, adding temperature is going to shift toward reactants./nIt will shift it in the endothermic direction using up the heat. Again, this is what we saw before. But now we have a different explanation for why. Again, a large activation energy barrier means that the rate constants are very sensitive to temperature./nIt is highly affected. If it is big, it is large. It needs temperature for the molecules to get over. Increasing the temperature has a big affect. Now molecules can do it. They can get over. This is why a large barrier means that a reaction is sensitive to temperature./nBig activation energy, big difference. Small activation energy, not such a big difference. less...

Description (Edit): Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 34/nTopics covered: /nKinetics (cont.)/nInstructor: /nProf. Catherine Drennan/nTranscript - Lecture 34/nAll right./nLet's continue then on this unit of kinetics. Today we are going to talk about temperature and we are going to talk about collisions and we are going to talk about activation energies and activated complexes./nAnd we are still in Chapter 13 in your book. When we started this unit on kinetics, we listed a bunch of things that can affect a rate of a reaction. And let's just review what we have talked about and what we have left to talk about./nWe talked about mechanisms of reactions. One step, two steps, fast steps, slow steps. That can affect the rate of the reaction. We talked about concentratio... more....