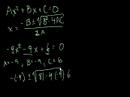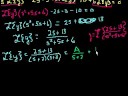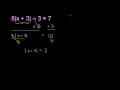Solving Inhomogeneous Partial Differential Equations
Solving Linear Inhomogeneous 2nd Order Partial Differential Equations Without Boundary Conditions/n As an initial application of the second order inhomogeneous linear ordinary differential equation particular solution formula, the purpose of this article is to demonstrate that important inhomogeneous partial differential equations may be solved without resort to initial or boundary conditions - at least until the final arbitrary constants determining step. The homogeneous parts of the solutions herein are well-known, place your attention on the inhomogeneous parts. The homogeneous parts are simply included (and short, indeed) for completeness. Of course, the reader may read beyond these pages into series solutions of all types, of which this author is also well acquainted with, but inclusion of these in these references is off point. After doing some math, working on a problem, a general solution to the radially symmetric inhomogeneous Helholtz or steady state Klein-Gordon equation is obtained, as well as Poisson’s equation. /nNext, the problem is generalized a bit, and the results are applied to the heat equation, time-dependant Klein-Gordon equation, and wave equation ... /n ... Thus, is shown that without resort to initial/boundary conditions, inhomogeneous solutions to the Helmholtz equation (including Poisson's equation), and certain cases of the heat, Klein-Gordon and wave equations may be obtained. And, these are the appropriate points to introduce the initial/boundary conditions to determine the arbitrary constants and establish the specific solutions. /n Thus, [1], has shown itself not only to be invaluable in solving ordinary differential equations of second (and indeed, arbitrary order), but also in solving important second order (and, clearly arbitrary order) partial differential equations. Links to all my books may be found at: /nhttps://sites.google.com/site/themathematicalnatureofreality//nhttps://sites.google.com/site/themathematicalnatureofreality/config/pagetemplates/books
Channels: Physics (General) Mathematics
Tags: partial differential equation Helmholtz equation Klein-Gordon equation heat equation wave equation Poisson's
Uploaded by: cloudmichael ( Send Message ) on 31-08-2011.
Duration: 3m 34s