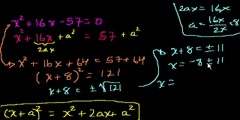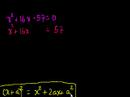Lec 13- Hilary: The Square Well
"Lec 13- Hilary: The Square Well"In this series of physics lectures, Professor J.J. Binney explains how probabilities are obtained from quantum amplitudes, why they give rise to quantum interference, the concept of a complete set of amplitudes and how this defines a "quantum state". Notes and problem sets here http://www-thphys.physics.ox.ac.uk/people/JamesBinney/lectures.html
Video is embedded from external source so embedding is not available.
Video is embedded from external source so download is not available.
Channels: Physics (General)
Tags: Lec 13- Hilary: The Square Well
Uploaded by: oxfordquantmmech ( Send Message ) on 09-09-2012.
Duration: 52m 31s
Here is the next lecture for this course
Completing the square
00:00 | 5271 viewsLec 43 - Completing the square
13:45 | 2345 viewsLec 112 - Problem involving angle derived ...
08:15 | 2230 viewsLec 14- A Pair of Square Wells and the Am ...
54:34 | 2442 viewsLec 62 - Chi-Square Distribution Introduction
10:23 | 2990 viewsLec 63 - Pearson's Chi Square Test (Goodn ...
11:48 | 3501 viewsLec 64 -Contingency Table Chi-Square Test
17:37 | 3139 viewsLec 15 - Punnett Square Fun
25:16 | 3860 viewsLec 9 - CA Algebra I: Completing the Square
13:48 | 2009 viewsLec 127 - Completing the Square 1
03:22 | 1871 viewsLec 128 - Completing the Square 2
05:24 | 1970 viewsLec 129 - Completing the Square 3
06:14 | 1755 viewsLec 130 - Completing the Square 4
09:31 | 1955 viewsLec 42 - Understanding Square Roots
01:21 | 2370 viewsLec 90 - Square a Binomial
03:38 | 2342 viewsNo content is added to this lecture.
This video is a part of a lecture series from of Oxford
Lecture list for this course
Lec 1- Introduction to Quantum Mechanics, Probability Amplitudes and Quantum States
Lec 2- Dirac Notation and the Energy Representation
Lec 3-Operators and Measurement
Lec 4 -Commutators and Time Evolution (the Time Dependent Schrodinger Equation)
Lec 5- Further TDSE and the Position Representation
Lec 6- Wavefunctions for Well Defined Momentum
Lec 7- Back to Two-Slit Interference, Generalization to Three Dimensions and the Virial Theorem
Lec 8- The Harmonic Oscillator and the Wavefunctions of its Stationary States
Lec 9 -Dynamics of Oscillators and the Anharmonic Oscillator
Lec 10- Transformation of Kets, Continuous and Discrete Transformations and the Rotation Operator
Lec 11- Transformation of Operators and the Parity Operator
Lec 12- Angular Momentum and Motion in a Magnetic Field
Lec 14- A Pair of Square Wells and the Ammonia Maser
Lec 15- Tunnelling and Radioactive Decay
Lec16- Composite Systems - Entanglement and Operators
Lec17- Einstein-Podolski-Rosen Experiment and Bell's Inequality
Lec 19- Diatomic Molecules and Orbital Angular Momentum
Lec 20 - Further Orbital Angular Momentum, Spectra of L2 and LZ
Lec 21- Even further Orbital Angular Momentum - Eigenfunctions, Parity and Kinetic Energy
Lec23 - Spin 1/2 , Stern - Gerlach Experiment and Spin 1
Lec 24- Classical Spin and Addition of Angular Momenta