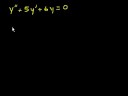A Particular Solutions Inhomogeneous 3rd Order...

7171 views

A Formula for Particular Solutions Of Inhomogeneous Linear Ordinary Differential Equations of Third Order/n As I have shown earlier in reference [6], a particular solution for inhomogeneous linear second order ordinary differential equations may be determined by the following short method. /n In this I have refrained from using the ‘s’ notation, and all other shortcuts to impress the fact that the particular solution formula is not just for some 2nd order ODE’s. And the formula is written, here, in a more compatible format. Please see reference [6] to view worked out examples, and my short table of 2nd order particular solutions video for even more, even more general ones. In the analysis of the 3rd order particular solution formula, the canvas becomes so full, even using the ‘s’ notation, that it becomes indispensible - especially in video format. The analysis goes much the same, only with far more terms. The major differences are at the end, where the 2nd order formula is applied, and the relationship between the homogeneous and particular solutions in the variant of the reduction of order technique. Finally, a formula for third order ODE particular solutions may be written. Four worked out examples follow, followed by part of a general table-type one. My 4th order formula is on video, now, and my arbitrary order book is available on kindle, now, too. As always: All my books are available on Kindle in digital format at amazon.com, and links to all my books may be found at the following websites https://sites.google.com/site/themathematicalnatureofreality/ https://sites.google.com/site/themathematicalnatureofreality/config/pagetemplates/books