A Small Table of Particular Solutions

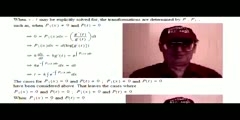
A Small Table of Particular Solutions For Inhomogeneous Linear Ordinary Differential Equations of Second Order... A formula for particular solutions to any linear second order inhomogeneous ordinary differential equations is presented, along with another way of producing them. Three useful general examples then follow, establishing the beginings of a table of particular solutions for linear inhomogeneous differential equations of second order, This firmly establishes this formula as preeminent above all the other techniques in obtaining fast results. The references, [2], [3], and [5] have been used to verify these results; and reference [6] further contains a pair of verifying worked out example solutions as well as a short proof. Again, powers of sines and cosines may be written as sums and differences of multiple angle sines and cosines, i.e. sums and differences of complex exponentials, so this formula may be applied immediately, as above. Clearly, also, this formula is a convenient starting point to prove that the standard forms of a particular solution are as generally presented in introductory ODE texts. As demonstrated above, it is no more computationally extensive than the methods of undetermined coefficients or variation of parameters; and certainly less so than the Wronskian and convolution methods. Computationally, this method must be much more compact in memory and execute faster; considering the particular solutions may be tabularized as above, and each of the possibilities jumped to and computed immediately - as opposed to the other methods being crunched out the old "mindless" ways. And, as an added bonus, using the above examples and techniques, this method makes creating text exercizes with solutions virtually effortless. All my books are available on Kindle in digital format at amazon.com, and links to all my books may be found at: https://sites.google.com/site/themathematicalnatureofreality/ https://sites.google.com/site/themathematicalnatureofreality/config/pagetemplates/books /n References [1] Kamke, E.; Differentialgleichungen Lōsungsmethoden Und Lōsungen, 3rd Ed., Chelsea Publishing Company, New York, N. Y.; 1959. [2] Nagle, R.K. , & Saff, E.B.; Fundamentals of Differential Equations and Boundary Value Problems; Addison Wesley Publishing Company, Inc.; Reading, MA; 1994. [3] Nagle, R.K. , & Saff, E.B., & Snider, A.D.; Fundamentals of Differential Equations, 5th Ed.; Addison Wesley Longman, Inc.; Reading, MA; 2000. [4] Polyanin, Andrei D. & Zaitsev, Valentin F.; Handbook of Exact Solutions for Ordinary Differential Equations, 2nd. Ed.; Chapman & Hall/CRC; New York, NY; 2003. [5] Zill, Dennis G.; A First Course in Differential Equations with Applications, 4th Ed.; PWS-KENT Publishing Company; Boston, MA; 1989. [6] SciVee: DOI: 10.4016/28294.01 , http://www.scivee.tv/node/28294 ; http://www.dnatube.com/video/6899/A-Particular-Solutions-Inhomogeneous-2nd-Order-ODE-Formula