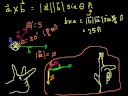
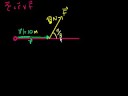
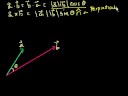
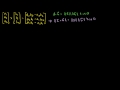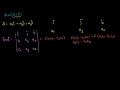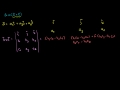Lec 29 - Dot and Cross Product Comparison/Intuition
Dot and Cross Product Comparison/Intuition Dot and Cross Product Comparison/Intuition
Video is embedded from external source so embedding is not available.
Video is embedded from external source so download is not available.
Channels: Mathematics
Tags: Dot and Cross Product Comparison/Intuition
Uploaded by: khanlinearalgebr ( Send Message ) on 10-09-2012.
Duration: 19m 14s
Here is the next lecture for this course
Lec 121 - Cross Product 2
10:53 | 2479 viewsLec 120 - Cross product 1
10:02 | 2478 viewsLec 122 - Cross Product and Torque
10:00 | 2723 viewsLec 136 - Dot vs. Cross Product
10:45 | 2285 viewsLec 27 - Linear Algebra: Cross Product In ...
15:47 | 2523 viewsLec 28 - Proof: Relationship between cros ...
18:09 | 3270 viewsCross Product of Vectors
02:33 | 4837 viewsWebsite Tutorial – Product Comparison
01:18 | 7789 viewsLec 141 - Vector Triple Product Expansion ...
14:25 | 2866 viewsLec 30 - Vector Triple Product Expansion ...
14:25 | 3317 viewsLec 8 - Cross Platform Mobile App Develop ...
01:02:43 | 3144 viewsRole of myosin cross-bridge in the contra ...
00:58 | 150216 viewsSarcomere Model Cross Sectional View
02:41 | 7089 viewsSolving For The Scalar Product And Vector ...
02:57 | 4111 viewsLec 16 - Derivative Intuition Module
03:58 | 3278 viewsNo content is added to this lecture.
This video is a part of a lecture series from of khan
Lecture list for this course
Lec 1 - Introduction to matrices
Lec 2 - Matrix multiplication (part 1)
Lec 3 - Matrix multiplication (part 2)
Lec 4 - Inverse Matrix (part 1)
Lec 5 - Inverting matrices (part 2)
Lec 6 - Inverting Matrices (part 3)
Lec 7 - Matrices to solve a system of equations
Lec 8 - Matrices to solve a vector combination problem
Lec 10 - 3- variable linear equations (part 1)
Lec 11 - Solving 3 Equations with 3 Unknowns
Lec 12 - Linear Algebra: Introduction to Vectors
Lec 13 - Linear Algebra: Vector Examples
Lec 14 - Linear Algebra: Parametric Representations of Lines
Lec 15 - Linear Combinations and Span
Lec 16 - Linear Algebra: Introduction to Linear Independence
Lec 17 - More on linear independence
Lec 18 - Span and Linear Independence Example
Lec 20 - Linear Algebra: Basis of a Subspace
Lec 21 - Vector Dot Product and Vector Length
Lec 22 - Proving Vector Dot Product Properties
Lec 23 - Proof of the Cauchy-Schwarz Inequality
Lec 24 - Linear Algebra: Vector Triangle Inequality
Lec 25 - Defining the angle between vectors
Lec 26 - Defining a plane in R3 with a point and normal vector
Lec 27 - Linear Algebra: Cross Product Introduction
Lec 28 - Proof: Relationship between cross product and sin of angle
Lec 30 - Matrices: Reduced Row Echelon Form 1
Lec 31 - Matrices: Reduced Row Echelon Form 2
Lec 32 - Matrices: Reduced Row Echelon Form 3
Lec 33 - Matrix Vector Products
Lec 34 - Introduction to the Null Space of a Matrix
Lec 35 - Null Space 2: Calculating the null space of a matrix
Lec 36 - Null Space 3: Relation to Linear Independence
Lec 37 - Column Space of a Matrix
Lec 38 - Null Space and Column Space Basis
Lec 39 - Visualizing a Column Space as a Plane in R3
Lec 40 - Proof: Any subspace basis has same number of elements
Lec 41 - Dimension of the Null Space or Nullity
Lec 42 - Dimension of the Column Space or Rank
Lec 43 - Showing relation between basis cols and pivot cols
Lec 44 - Showing that the candidate basis does span C(A)
Lec 45 - A more formal understanding of functions
Lec 46 - Vector Transformations
Lec 47 - Linear Transformations
Lec 48 - Matrix Vector Products as Linear Transformations
Lec 49 - Linear Transformations as Matrix Vector Products
Lec 50 - Image of a subset under a transformation
Lec 51 - im(T): Image of a Transformation
Lec 53 - Preimage and Kernel Example
Lec 54 - Sums and Scalar Multiples of Linear Transformations
Lec 55 - More on Matrix Addition and Scalar Multiplication
Lec 56 - Linear Transformation Examples: Scaling and Reflections
Lec 57 - Linear Transformation Examples: Rotations in R2
Lec 58 - Rotation in R3 around the X-axis
Lec 60 - Introduction to Projections
Lec 61 - Expressing a Projection on to a line as a Matrix Vector prod
Lec 62 - Compositions of Linear Transformations 1
Lec 63 - Compositions of Linear Transformations 2
Lec 64 - Linear Algebra: Matrix Product Examples
Lec 65 - Matrix Product Associativity
Lec 66 - Distributive Property of Matrix Products
Lec 67 - Linear Algebra: Introduction to the inverse of a function
Lec 68 - Proof: Invertibility implies a unique solution to f(x)=y
Lec 69 - Surjective (onto) and Injective (one-to-one) functions
Lec 70 - Relating invertibility to being onto and one-to-one
Lec 71 - Determining whether a transformation is onto
Lec 72 - Linear Algebra: Exploring the solution set of Ax=b
Lec 73 - Linear Algebra: Matrix condition for one-to-one trans
Lec 74 - Linear Algebra: Simplifying conditions for invertibility
Lec 75 - Linear Algebra: Showing that Inverses are Linear
Lec 76 - Linear Algebra: Deriving a method for determining inverses
Lec 77 - Linear Algebra: Example of Finding Matrix Inverse
Lec 78 - Linear Algebra: Formula for 2x2 inverse
Lec 79 - Linear Algebra: 3x3 Determinant
Lec 80 - Linear Algebra: nxn Determinant
Lec 81 - Linear Algebra: Determinants along other rows/cols
Lec 82 - Linear Algebra: Rule of Sarrus of Determinants
Lec 83 - Linear Algebra: Determinant when row multiplied by scalar
Lec 84 - Linear Algebra: (correction) scalar muliplication of row
Lec 85 - Linear Algebra: Determinant when row is added
Lec 86 - Linear Algebra: Duplicate Row Determinant
Lec 87 - Linear Algebra: Determinant after row operations
Lec 88 - Linear Algebra: Upper Triangular Determinant
Lec 89 - Linear Algebra: Simpler 4x4 determinant
Lec 90 - Linear Algebra: Determinant and area of a parallelogram
Lec 91 - Linear Algebra: Determinant as Scaling Factor
Lec 92 - Linear Algebra: Transpose of a Matrix
Lec 93 - Linear Algebra: Determinant of Transpose
Lec 94 - Linear Algebra: Transpose of a Matrix Product
Lec 95 - Linear Algebra: Transposes of sums and inverses
Lec 96 - Linear Algebra: Transpose of a Vector
Lec 97 - Linear Algebra: Rowspace and Left Nullspace
Lec 98 - Lin Alg: Visualizations of Left Nullspace and Rowspace
Lec 99 - Linear Algebra: Orthogonal Complements
Lec 100 - Linear Algebra: Rank(A) = Rank(transpose of A)
Lec 101 - Linear Algebra: dim(V) + dim(orthogonoal complelent of V)=n