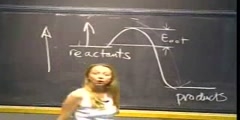Chemical Science - Discovery of Nucleus - Lecture 2
Chemistry > Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 2/nTopics covered:
/nDiscovery of Nucleus/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 2/nSo let's get going today. And what we were talking about last time is the discovery that the atom was not the most basic constituent of matter, that there was a particle that was even less massive than an atom./nAnd that is the electron. But today we're going to discover the nucleus. And so this is 1911. And this is Ernest Rutherford in England. And what he was interested in doing was studying the emission from these newly radioactive elements that were being discovered./nSo the emission from radium, for example. What he did was he got a sample of radium bromide from his friend Marie Curie. And what was known was that this radium bromide emitted something called alpha particles./nAnd the exact nature of these alpha particles was not known. However, what was known was that they were heavy particles, that they were charged and that they were energetic. And, of course, today we know what these alpha particles are./nThey are helium double plus, a helium with two electrons removed. All right. So he got this radium bromide. And alpha particles are being emitted from the radium bromide. And he had some kind of detector way out here which detected these alpha particles./nAnd what he found was that at the detector there were about 132,000 alpha particles per minute. That was the count rate that he was able to measure. And then, because he was just trying to figure out what is the nature of these particles, he did this experiment./nHe took a gold foil, a really thin gold foil here, really thin meaning 2 times 10 to the negative 5 inches. That's two orders of magnitude thinner than the diameter of your hair. I've always wondered how he handled that./nThat is pretty thin. But he put that in there. And, low and behold, the count rate that he measured, once this gold foil was in place, the count rate was still 132,000 alpha particles per minute. It appears that all of the alpha particles that were being emitted just went through the foil right to the detector./nIt didn't even seem like those alpha particles knew the foil was there. The same count rate. It doesn't sound like a very interesting experiment, but at that time he was working with a person named Geiger, a post-doc named Geiger./nThe same Geiger as the Geiger counter. And Geiger wasn't too happy about the results of these experiments. And, in addition, Geiger had this undergraduate student hanging around the lab. This undergraduate named Marsden./nAnd Marsden was really excited about doing science. He just hung around there. He really wanted to do something. And Geiger was, jeez, what am I going to do with this guy? Geiger goes to Rutherford and says I've got Marsden here, he really wants to do something, what should I do with him? And Rutherford said well, OK, let's have him build a detector that can swing around that gold sample./nLet's have him build a detector that will rotate around such that the detector can be positioned this way so that we can look for any alpha particles that might be backscattered, backscattered meaning scattered back in the direction from which they came./nAnd Geiger said ah-ha, this will keep this guy busy and not in my hair. No problem. So he goes down to Marsden, Marsden is all excited to build this detector. He builds the detector and gets Geiger, OK, we're ready to go./nLet's try this. And so they put the radium bromide there in this arrangement. They're sitting there at the detector and they hear tick, tick, tick, etc. Hey, particles at the detector. And they go oh, well, that must just be a general background./nSo what they do then is they take this gold foil away so that presumably all the particles are going in that direction and they listen and they hear nothing. And they put the gold foil back. And they listen and they hear tick, tick, tick, etc., 20 alpha particles per minute./nAnd they then pick another foil, platinum foil, basically the same result. They go up to Rutherford, they get him down in the laboratory, and Rutherford is looking over their shoulder, tick, tick, tick, etc./nHey, there are some alpha particles coming off. Not many. Look at what the probability here is of the backscatter. Hey, that probability, we can calculate that. The probability is simply the number of backscattered particles, 20, the count rate of the backscattered particles, 20, over the count rate of the incident number of particles, 132,000./nThat probability is 2 times 10 to the negative 4. Not large but not zero. There is something coming off. And Rutherford was amazed. And what he wrote later on was that this experiment was quite the most incredible event that has ever happened to me in my life./nIt was almost as incredible as if you fired a 15 inch shell at a piece of tissue paper and it came back and bit you. So how does he interpret that experiment? Well, what he said is that since most of these alpha particles went right through this foil to the detector that must mean that those gold atoms that make up that gold foil must be mostly empty./nSo the picture is that you've got this gold atom here. And he knew, roughly speaking, how large that gold atom was. He knew it to be about 10 to the negative 10 meters. But what he was proposing is that these helium ions going through, these alpha particles are just going right through that volume because most of the atom -- And he knew that there were electrons in this atom because he knew about the electrons already, most of that atom is empty./nHowever, occasionally, once in a while, not very often but occasionally these helium ions, these alpha particles, what happened? Well, occasionally they hit something very massive in that atom. And when it hit that massive part of the atom it reflected, it scattered back into the direction from which it came./nAnd from knowing what these scattering probabilities are and from knowing roughly the size of this atom and the thickness of the gold foil, he could calculate what the diameter of this nucleus was. And that number came out to be about 10 to the negative 14 meters, the diameter of this heavy massive part of the atom./nNow, he called that massive part, he called it the nucleus. He called it a nucleus in analogy to the massive center of a living cell. That's where that name comes from. And this number of 10 to the negative 14 diameter, that's a good number to know, the relative size of the nucleus./nAll MIT students should know that. He also knew that that nucleus really had to be positively charged. Why did it have to be positively charged? Well, because he knew that these atoms were neutral, he knew already that an electron was part of an atom./nAnd so this nucleus had to be positively charged. And, in addition, he made some very sophisticated measurements of the angular distribution of the backscattered alpha particles. And from those measurements of the angular distribution, he was able to back out the fact that this nucleus had a charge of +Z, where Z is the atomic number, times unit charge e./nSo his model is the Z electrons filled this volume, this sphere effectively of 10 to the negative 10 meters in diameter. The electrons filled that up, but somewhere in the center there is something that is very small and very massive that has a diameter of 10 to the negative 14 meters./nBecause occasionally that alpha particle hit that massive part so most of the mass of the atom is in this nucleus. Now, isn't this a great UROP project for Mr. Marsden? What did he do? He discovered the nucleus./nFantastic. I also want to tell you that this kind of Rutherford backscattering experiment here is also the basis of the experiment that was done to discover the quark, the quark that is the elementary particles that make up the proton, the neutron./nSame idea. There is a high energetic particle that comes into the proton and backscatters from the quark essentially. That is an experiment carried out by one of my colleagues in the Physics Department, Jerry Friedman and Henry Kendall./nHenry Kendall has since passed away. But the same idea. It's really the Rutherford backscattering experiment that was done. All right. Well, now it is time for us to do our own Rutherford backscattering experiment./nAnd the way we are going to do that is we're going to be scattering off of this lattice here, this lattice of these Styrofoam balls. These Styrofoam balls are gold atoms, gold nuclei, and then the space around them is where the electrons are./nSo this is one monolayer of gold atoms. Now, this scale is a little wrong. The real scale would be if we had a pinhead in the center of this room and then the rest of the room was the atom and then there would be another room 1051 with a pinhead in the center of that./nThat's the real scale, but the fact that the scale isn't right that's OK. We are going to be able to understand the principle here. And what we want to do is we want to be able to measure the diameter of these Styrofoam balls or the diameter of those gold nuclei./nAnd we're going to measure it by measuring the probability of backscattering. And the way we're going to measure the probability of backscattering is we're going to take these ping-pong balls, and they are going to be our alpha particles./nAnd we are going to aim them at the lattice. And we are going to have a total of 287 pin pong balls, or 287 alpha particles. And so the probability of backscattering will be simply the number backscattered over the total number incident, which will be 287./nSo this is what we are going to measure. Now, the next thing we have to do is that we've got to relate this probability of backscattering. We are going to have to relate it to the diameter of those nuclei./nHow do we do that? Well, the probability of a particle backscattering is simply going to be the total area of this crystal, there's our crystal, the total areas of this. Now, you've got to ignore these aluminum blocks here because this piece of equipment comes from my laboratory./nAnd I pressed it into service for this demonstration. This has nothing to do with the demo that we're going to put here. It's just structural because this is my manipulator puller-outer from our machine./nSo you've got to ignore those, but that whole area there is equal to 2,148 square inches. And now the probability of that backscattering is this total area of the nuclei to the total area of the crystal./nAnd the total area of the nuclei then is just the sum over all nuclei, and there are 119 of them here. So i=1 to 119 of the area of each one of the nuclei. And so that is just 119 times the crossectional area of these nuclei actually, which is p d2/4 and this is all over 2,148./nThat's the probability. This is the diameter of the nuclei. And now I am going to rearrange that and solve for the diameter. And when I do that I get 4.79 times PΩ. If I measure the probability of backscattering by this, measuring the number of backscattered balls over the total number we throw at it then I can calculate the diameter of the nuclei, the diameter of those Styrofoam balls./nThat is the idea. Now, you're going to do this experiment. And so now the TAs are going to give you all a pin pong ball or two. Come on. We need to distribute the pin pong balls. Here's the deal./nWhat you have to do is you have to aim to hit this lattice. That's all you've got to do. Then you have to watch your ball, and you have to see if it scatters back to you. Now, what doesn't count is if you hit these steel bars and it scatters back./nThat doesn't count, OK? It also doesn't count if the ball hits the Styrofoam but it continues going in that direction. Your pin pong ball has to actually scatter back at you to count. And then, when we get all done, I am going to ask whose ball backscattered./nThat's what we've got to do. Now, some of you aren't in the optimal position to hit the lattice. I invite you to come down and get a little closer. That is OK. Now, are you roughly ready? Yeah. All right./nBut there is one other piece of information that is very important that I have got to tell you. And that is that only fools aim for their chemistry professor. [LAUGHTER] OK, go to it. Watch your ball./nOK. Have all the alpha particles been launched? Yes. Fantastic. All right. Now comes the moment of truth. How many of you had an alpha particle that backscattered? OK, so now I've got to count./nKeep your hands up because there are some lights that make it a little hard for me to see. Anybody in this section here? Yes. One, two, three, four, five. Six. Anymore? Did I get everybody? That's it? Six alpha particles that backscattered./nOK, so now we have to calculate some probabilities here. The probability of backscattering is the number that backscattered. Six divided by 287 and that gives me 0.021, carrying one extra significant figure./nAnd if I now take that probability and I plug this into here, I've already done a calculation. I got a table here. I find that that diameter to the correct number of significant figures is 0.7. And the actual diameter of these balls is 0.8./nSo you guys did a very great job. [APPLAUSE] All right. This works. That's how they calculated the diameter of the nucleus. That's it. Nothing else involved in this. That is the principle behind how it was done./nVery simple. That is the principle behind how the quark was discovered and the size of the quark was revealed. That is terrific. Now, we've got the problem that the scientific community had in 1911, 1912, right after the discovery of the nucleus./nAnd the problem is now we know the atom has got a nucleus, we know it has got an electron, what is the structure of the atom? How does the electron and the nucleus hang together? In particular, what we have to do is we have to ask what is the force of attraction that keeps the nucleus and the electron together? We are going to talk here about this classical description of the atom./nAnd we've got to talk about the force of the interaction first. Well, there are four known fundamental forces. What is the force that is the weakest force? Gravity. Absolutely. What is the force that is the next stronger force? Electromagnetic./nAbsolutely. What is the next stronger force? Weak force. And the next force? Strong force. All right. The weak and the strong forces here, these are intranuclear forces within the nucleus. That's what keeps the protons and neutrons and the quarks together./nFor the most part, the weak and the strong force don't have an effect in chemistry, with the exception for beta decay, for some radioactive elements. That's where you need to think about, in particular, the weak force./nGravity also -- Well, gravity actually has no known consequence for chemistry. It doesn't mean that there isn't one, but it has no known consequence for chemistry. All of chemistry is tied up in this force, the electromagnetic force./nNow, what I am going to do is I am going to simplify it just a little bit and just call this the Coulomb force. And why I am going to do that is going to be a little more obvious when you get to 8.02./nBut I am going to call it the Coulomb interaction. And we know what the Coulomb force law looks like. The Coulomb force law is the following. Say I have a positive charge, which is my nucleus. I am going to call that force plus e./nAnd at some distance R, R is the distance now, between that nucleus and the negatively charged particle which is my electron. I can describe the force of attraction between this electron in the nucleus by the following expression./nThat force, which is a function of the distance between the two charges, is just the magnitude of the charge on the negatively charged particle times the magnitude on the positively charged particle over 4p epsilon knot r2./nNow, I am going to treat this force, just for simplicity purposes right now, as a scaler. I am not going to talk about the direction, but because this is a force between a positive and negative charge this is an attractive force./nThis epsilon down here is the permittivity of the vacuum. It is in there for doing our unit conversion correctly. That is all I will say about it. Maybe you will talk a little bit more about it in 8.02./nAnd then, finally, here is the r2 that is the important part. That is the distance between the electron and the nucleus. And what I want you to notice here, I don't need the screen down yet. Hello./nShe just switched it? Oh, all right. Sorry. It looks like I'm not going to get to it, actually. Thank you. What I want you to notice here is that when R goes to infinity, what is the force going to do? Zero./nWhen those two particles are infinitely far apart, you've got an infinity in the denominator, this force is zero, there is no attraction between them. But when R goes to zero, what does that force do? Infinity./nWhen R is zero there is an infinity large force. And in between what is happening is that the closer the particles get to each other the larger the force. The more attraction there is. The more they want to be even closer to each other./nAll right. Now, what this equation is telling me is simply what is the force of attraction between the nucleus in an electron for a fixed distance r? In other words, if I were holding the electron and the nucleus in my hands at some distance R that equation would tell me what the force was./nAnd you can bet that in order to keep them apart, I would really have to be pulling like this. You'd feel it. But you also know that if you let them go what would happen is that they would move toward each other./nWhat this equation does not tell us is how they move toward each other. It does not tell us how R changes with time. It doesn't tell us anything about R as a function of time. Although we know the force law, we don't know anything from that force law about how those two particles move under influence of that force./nAnd so what we need is we need an equation of motion. And the equation of motion that was known at that time is, of course, Newton's equations of motion, Newtonian mechanics, classical mechanics, the mechanics that governs the motion of all bodies around us that we see easily and astronomical bodies./nIn particular, Newton's second law, F = ma, this force equal the mass of the particles times the acceleration. And, of course, in this acceleration term, well, I think you know what's in there. In that acceleration term, let me just write it out, the acceleration then is the change in velocity with respect to time and the velocity is the change in the position R with respect to time./nSo we have a second derivative here. What is in this force law is a way to get R as a function of time under influence of this force. So we take this force and we substitute it in here and we would be able to solve a differential equation for how those two bodies move under influence of that force./nAnd when we solve this equation we would know exactly where the two bodies would be at all times. As long as we know where the bodies were when they started out, using that force law and this equation of motion we could tell you what R would be for all future times./nThat's called deterministic. That's classical mechanics. Well, we're not going to do it but we could actually set up a differential equation and solve for what R of T is using that force law. We could do that./nAnd if I did that and if I started out the electron and the nucleus at one angstrom from each other like they are, roughly speaking, in an atom, what would happen is that that electron would plummet into the nucleus in 10-10 seconds./nIf I solved these equations, I would find that R would be equal to zero and T equal to 10-10 seconds. We've got a problem here. The problem is that this classical physics, Newton's second law and the force law, it is predicting that after 10-10 seconds the electron and the nucleus are on top of each other, they've neutralized each other./nWe no longer have an atom that has a diameter of 10-10 meters. That's contrary to our observations. This is saying the atom collapses in 10-10 seconds. But what we see is that the atom seemingly lives forever./nSo we've got a big problem here. Yes they did in 1911, 1912. And the problem is that this kind of classical way of thinking does not predict our observations. It does not predict the fact that the atom lives together, it lives forever./nIt says the atom falls apart. So it could be that the Coulomb force law is wrong or it could be that this equation of motion is incorrect. And of course what's going to turn out is that this equation of motion does not work for electrons in atoms./nYou cannot use classical mechanics to describe the electron within the atom. We need a new kind of mechanics, and that new kind of mechanics is going to be quantum mechanics. That is where we will pick up on Monday./nHave a nice weekend.
Tags //
Chemical Science Nucleus
Added: April 16, 2009, 10:17 pm
Runtime: 2114.80 | Views: 21060 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science-Atomic Theory of Matter lecture 1
Home > Courses > Chemistry > Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 1/nTopics covered:
/nAtomic Theory of Matter/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 1/nAll right. What we are going to do today is I am going to start talking about the development of atomic theory. So, in the next few minutes, I am going to wiz through the observations that led to the belief that atoms were the most basic constituent of matter./nAnd then what we are going to see is that the atom can actually be split up, that the atom is not the most basic constituent of matter, that there is at least an electron and a nucleus. And we are going to start talking about what are the fundamental principles that have to obtain in order for that electron and nucleus to hang together to remain an entity./nAnd what we are going to see is that we are going to have to understand a new kind of mechanics to understand how that electron and nucleus hang together. And then further on in the course we are going to see we are going to need that new kind of mechanics to also understand how two atoms hang together, how two atoms bind to form a molecule./nAll right. But today I will lecture for the first two-thirds or three-quarters of the course and then I will stop. And then I will introduce the rest of our teaching team. And we will talk about the mechanics of the course./nWe will talk about the expectations of the course and some details like that. OK, so let's get going here. And now we could turn the lights down because I am going to use the slide here in the front./nAll right. The ancient Greek philosophers. They certainly were known to have pondered whether matter can be divided endlessly into smaller and smaller pieces or whether there was a point at which you couldn't divide matter any further./nAnd Aristotle here, well, he was one of the philosophers who argued that matter could be divided into smaller and smaller particles, chopped up into smaller and smaller pieces, add infinite, matter was divisible./nThis is called the Continuum Theory of Matter. Continuum because you don't have any discrete points. It is a continuum. No boundaries. But there was a contrary philosophy, a contrary philosophy heralded by Democritus who actually was about a hundred years older than Aristotle./nAnd he held that matter indeed was composed of individual discrete particles. These discrete particles he called ·tomos. A for not, tomos for divisible. That is the origin of our word, of course, atoms./nNow, in the 4th, 5th century BC, there wasn't much evidence one way or the other for either one of these philosophies. And I call it a philosophy because it was a search for understanding reality by a speculative as opposed to an investigational or observational means./nBut, for whatever reason, it was Aristotle here, his continuum theory of matter prevailed all the way to the 17th century. And here, in fact, he is depicted by Raphael on a fresco on the walls of the Vatican holding court, the continuum theory of matter./nBut, just about at the same time at which Raphael painted this picture, there were observations. A set of observations that were being made that began to point out that matter wasn't really behaving and reacting like a continuum, that matter was behaving more like it had some discrete nature to it./nWhat were those observations? Well, one of them was by this gentleman here, Robert Boyle. And guess what his formal occupation was? Chemistry? That's a good guess, but his formal occupation was a theologian, as most scientists were at that time./nAnd you, of course, know him for the empirical observation that the pressure times the volume is constant as long as the temperature is constant. But he actually advanced one of the first ideas of an element./nAnd that is he called an element a certain primitive unmingled body. And that somehow you can take these primitive unmingled bodies and put them together to form a perfectly mixed boy, a compound, a molecule./nSo, this was one of the first ideas of elements that come together to form molecules. And then there was this gentleman, Joseph Priestly. Guess what his occupation was? He was a priest, of course./nAnd what did he do? Well, he looked at reactions with deep logisticated air, deep logisticated air reacting with materials. And what he observed was that these materials reacted more vigorously in deep logisticated air./nWell, what is deep logisticated air? Well, of course, now we know deep logisticated air is oxygen. It is air with the nitrogen predominantly removed. But it really took this gentleman, Lavoisier, to really understand what Priestly was doing in his experiments./nAnd what Lavoisier realized is that this deep logistic air was kind of adding to the material when it did this reaction. And he made those observations, or he came to those conclusions by doing some very careful measurements of the mass before the reaction, so the mass of the deep logistic air plus the mass of the material./nAnd he found that indeed the mass after the reaction was equivalent to that before the reaction. And so he was one of the first individuals to realize that a chemical reaction can be written down analogous to writing an algebraic equation./nWell, Lavoisier also did a lot of work with isolating elements. He identified 17 metals and 9 nonmetals as elements. Well, for all of his efforts, we all know what happened to Lavoisier. Because of his connection to the French monarchy, the judge at his trial claimed that the republic has no use for savants./nLagrange at that time, a French mathematician said it took but a moment to cut through that head but it will require a hundred years to produce another like it. Well, there was another Frenchman at that time, J.L./nProust. He was a little more politically savvy. He high-tailed it over to Spain and led a long and healthful life as a professor in Madrid. But what he did was he did some experiments. And he observed that when two or more elements combine, well, they combine to form a compound, they always combine in definite proportions by weight and it didn't matter what the method of preparation was./nAnd, because he made this observation over and over again with many different elements, this became known as the Law of Definite Proportion. Again, some indication that matter had a discrete nature to it and it wasn't just the continuum./nSome numbers were involved here. But it really took this guy, John Dalton, English schoolteacher with a lot of interests. He was aware of the observations of Boyle and Priestly and Lavoisier and Proust./nAnd what he realized was that he could begin to understand all of those observations if he went back all the way to Democritus and Democritus' idea of ·tomos or atoms, these individual discrete particles of matter./nAnd so he set forth some postulates, some postulates which of course now are known as Dalton's Atomic Theory. But what he said was that each element is composed of atoms. He said that atoms of any given element are identical./nHe said that compounds form when atoms are more than one element combined. And he realized, of course from Lavoisier's observations, that atoms are neither created nor are they destroyed. Now, just an aside, John Dalton with his breadth of interest, he also was the first individual to document color blindness in human beings./nAnd, in fact, we do call color blindness Daltonism. See, we are getting you ready for medical school already. But what I want you to recognize here is that Mr. Dalton didn't actually do any of the experiments himself./nAlthough, from what I know of him, I think he could have done the experiments himself, but rather he was aware of the seemingly disparate observations made by Lavoisier and Boyle and Proust. And he just said well, you know, if I take those observations and I use this framework, well, then I can understand them./nThey make sense within this framework. And this is a powerful approach in science. A lot of science progresses this way. That is that there is this collection of seemingly disparate observations, and then all of a sudden somebody comes along and sees an organizing principle in all of those observations and puts forth them these postulates./nThat is what Dalton did here. Now, of course, these postulates weren't accepted immediately. And rightfully so because they were just postulates, they needed further substantiation. And that further substantiation came in terms of the work by this gentleman, Joseph Gay-Lussac, the Law of Combining Volumes./nIt came by the work of this gentleman. This gentleman is Lorenzo Romano Amadeo Carlo Avogadro's hypothesis. And, of course, you can all read Italian, so you can read what is on the stamp here, right? It just says equal volumes of gas under the same conditions of temperature lead to the same number of molecules./nSee, you didn't know you could read Italian but there it is. And further substantiation for this idea of an atom and the discreteness of matter came from this gentleman Ludwig Boltzmann. Gas Kinetic Theory./nHe proposed that well, you know, pressure, that must be due to these atoms that are moving around and hitting the walls of a vessel, those impacts give rise to the pressure that is exerted on the walls of that vessel./nAnd then, finally, it took this gentleman Cannizaro, and it took his statesmanship. Because what Cannizaro did, and now this is later 1800s or so. What Cannizaro did was that he got the scientific establishment at that time./nAnd the scientific establishment at that time, of course, was this small group of pale males. But he got them to listen to Dalton's Atomic Theory and then the ensuing experiments of Avogadro and Gay-Lussac, etc./nAnd, finally, he got them to say yes, there is something right about this Atomic Theory of Matter, the idea that mass was made up of discrete particles called ·tomos or atoms. Well, nowadays we, of course, can actually image individual atoms or molecules./nAnd what you see here is an array of 28 CO molecules. And these 28 CO molecules are arranged in the form of a little man or a little woman, I will let you figure it out, but these are CO molecules sitting on a platinum surface./nAnd so each one of these orange balls here is a CO molecule, but when CO binds to a platinum surface it does so with the carbon end down and the oxygen end up. And there is a really good reason for why that is the case, and we will talk about that when we talk about molecular orbitals./nWhat you are seeing here is really just the tops of the CO molecules. You are seeing the oxygen end of the CO molecule. All right. Well, this image here was taken by something called a scanning tunneling microscope./nAnd, I am sorry to say, but this was actually invented just before you were born. And it was invented, it was actually worked on by Binnig and Rohrer, and they won a Nobel Prize for their work. And the way the technique works is the following./nLet me have the board lights here. I am going to do some board work. What you do to do this is that you take a tungsten wire, and you do a little chemistry. You etch the tungsten wire down to as fine a tip as you can./nYou put it in some potassium hydroxide, you send some current through it, do a little electrochemistry, and what you will get then is a pretty fine tip at the end of this tungsten wire. But then what you do is you take that tungsten wire and you attach it to a piezoelectric crystal./nA piezoelectric crystal, and let me put it this way here, a piezoelectric material is some material that if you put a voltage across it, it expands a little bit, a little bit meaning 10, 20 angstroms./nAnd so now, if you attach the tungsten wire to that material, you have some control on the angstrom scale. So, that is what happens in order to move that tip around. But then what you do is you take this tip and you bring it, say, within 5 angstroms of the top of this CO molecule./nIf I have my platinum surface here and my carbon here and here is my oxygen, what I am going to do is I am going to bring this tip, say, within 5 angstroms here of this oxygen and of the CO molecule./nAnd then I am going to put a negative voltage on this tungsten tip here. And I am going to take the CO molecule, I am going to take the platinum surface and I am going to ground it. Now, in this tungsten tip there are, of course, electrons./nAnd, since this is a metal, metal has a characteristic where some of those electrons are not strongly bound to the nucleus. They actually roam around the solid. And this is a high energy state. Given that electrons are negatively charged and they are in an environment of this negative potential that is a rather high energy state for those electrons./nSo, if I were to draw an energy level diagram here, this is energy, and I am going to represent those electrons on the tungsten tip, it is going to be at a sum high energy level. This is electrons on the tungsten./nHowever, there are also some electrons down here and they are at ground potential. These electrons are at a lower energy, so I am going to draw an energy level representing them. This is the electrons on the platinum./nAnd so this coordinate here is kind of like a distance. So, this is the electrons on the tungsten, over here the electrons on the platinum. And what these electrons on the tungsten tip would like to do is to be here on the platinum because that is a lower energy state, but the problem is that there is a gap right here./nThere is no material between the tip and the oxygen end of the CO molecule. If you do it in a vacuum, there is a vacuum here, there is a vacuum gap. And so for the electrons to go from here to here, well, there is a very large barrier./nThis is a very high energy state if an electron were in between this gap here. I am going to represent that energy change as the electrons go from the tungsten tip to the platinum surface as a barrier like this, a very large barrier./nNow, you have seen these kinds of we call them reaction coordinates in chemistry in high school. That is you have seen situations where we might have, if we are doing an energy level diagram, this is the energy of the reactants out here./nThis is the energy of the products. And in between there is this activation energy barrier that we call Eact. In other words, you have to put energy into the system. In order to get the reaction to go, you have to put energy into the system before you get any energy back out./nAnd that is what happens in a chemical reaction, we put energy into the system before we make it go or can make it go. But in this particular case, the electrons, they don't behave like most reactants./nThe electrons right here, you know what they do? These electrons, they go right through that barrier. They don't care that there is a brick wall there. They just go right through the barrier. We call that tunneling./nAnd how in the world can that happen? Well, that can happen because electrons, unlike most atoms and molecules over here, are quantum mechanical particles. And they do not obey classical mechanical rules./nAnd that is a subject that we are going to start talking about today and tomorrow and for the next few days. These electrons, they just tunnel right through that barrier and get over here to the other side./nThat means, in this experimental setup, if I were to connect a wire from this tungsten tip here to the platinum, and I put in an ammeter right there, so I measure the current, I would be seeing some current flow, some measure of this flow of electrons from the tip to the tungsten./nAnd so that is what is done in the technique. But, now, how do you get this image that I showed you earlier from this kind of arrangement? Well, what you do is you now take this tungsten tip and you mount it on a piezoelectric crystal./nI forgot to tell you sometimes piezoelectric crystal, quartz is a piezoelectric, barium titanate is a piezoelectric. But you mount it on a piezoelectric crystal that will allow you to move from side to side./nI move now my tungsten tip over a little bit. And I know exactly how much over I moved it because I have calibrated by piezoelectric crystal. But now what do you see? Well, if you just moved it over, you didn't change the vertical distance, if you just moved it over, what do you think would happen to the current here? Decrease./nIt would absolutely decrease. Why? Because you now have changed the distance between the oxygen end and that tungsten tip. Over here, on this diagram, you made this barrier thicker. And the thicker you make it, the more difficult it is for those electrons to get through, so the current is going to go down./nIn order to bring the current back up, what you are going to do is you are going to take that tungsten tip and you are going to move it down slightly so that the distance now, between the tip and the oxygen, is going to be the same as it was in this particular position from here to here./nSo, then you bring the current back up. But, again, you know exactly how far down you moved that tip and how far over you moved that tip. You have got now two points. Now we have got to keep going./nWhat are we going to do to scan? Well, we're going to move this tungsten tip over again. And, again, the current in this particular case is going to go down. In order to bring it back up, you are going to move this tip further down so that the distance between here and here is the same as it was originally./nSo, reestablish the current. But, again, you know exactly how far down and how far over you moved the tip. And then what you do, you assign a different color to the different distances above the CO molecule./nAnd, if you assign different colors, you can get this image. For example, if we can dim the lights on the blackboard again, we will look at the slide. If the tip is very far from the surface, we would give it kind of a whitish color./nAnd as it gets closer and closer to the surface, we give it a darker and darker orangey color. And then finally, when it is so far down that it is actually in contact or tunneling to the platinum, we give it a blue color./nSo, that is how you get this image. That is the basis of this technique. Now you also notice that these CO molecules have a peculiar arrangement. And this is not due to, in the most au courant language, intelligent design./nRather this is due to a very patient experimentalist, i.e. graduate student, who spent 24 hours putting these CO molecules into this particular position. How did he do that? Well, he did it in the following way./nHe first took a few CO molecules and put them anywhere on the surface, just to expose the surface to some gas, and then he imaged the surface to figure out where they were. And so if these CO molecules -- My soccer balls are the CO molecules./nAnd if my foot here is the tungsten tip. You just imaged the surface to figure out where they were, because we knew where they were. Then he has got to move these CO molecules. He brings the tip close to one of the CO molecules./nAnd then, if you put a voltage pulse on that piezoelectric and actual jerk the tip, you can jerk it such that you hit the CO molecule and it goes flying away. That is nice, but now where did it go? Well, in order to find out you have to image the whole surface again./nAnd you would find that it is somewhere all the way over here. Now you really want it over there, so you repeat the operation. Well, 24 hours later you get this little man. [LAUGHTER] And I know it was 24 hours later./nIt is going to be a while before this kind of nanotechnology assembling a molecule by a molecule beats the synthesis in a beaker to put the molecules where you want them. But, even though this kind of visual observation of atoms and molecules really was impossible a hundred years ago, the evidence that I alluded to or quickly went through earlier was really quite compelling for the existence of atoms./nAnd the observation or the belief that the atom was the most basic constituent of matter, the elementary particle. You couldn't have anything smaller than an atom. And, in fact, at the end of the last century, it was generally believed that the theoretical structure of the universe was complete./nNature was understood. There were no more discoveries to be made. And, after all, there were, by this time in the last 1800s, a lot of advances. Well, Newtonian mechanics, that had already been known for 250 years, mechanics that guides the motion of all bodies around us, even astronomical bodies./nThermodynamics was completely developed. Statistical mechanics was developed, statistical mechanics which relates the microscopic description of the behavior of matter to the macroscopic description of the behavior of matter./nAnd also there were these optics experiments of Young, Freznel and Hertz that seemed to put to rest the question of whether or not light was a particle or a wave. Boy, those experiments seem to be absolutely conclusive that light was a wave./nThose experiments demonstrated Maxwell's equations, Maxwell's equations that unified the field of optics and electromagnetism. So, by this time there were all of these accomplishments. The idea was that everything was done, and the idea that was remaining, that the work that remained was largely to investigate the next decimal place./nEverything else was done. However, at the same time, by the late 1800s, there began to be two sets of observations, two tracks of observations that if you look closely began to illustrate that maybe things weren't quite so clear./nMaybe things were quite as well understood. And what were those observations? Well, one of those observations is the discovery, that we are going to start looking at today, that the atom is not the most basic constituent of matter, that you can take an atom apart into an electron and a nucleus, at least an electron and a nucleus./nSo, that is one track. The other track is that light appeared to behave in some cases like a particle and not a wave. And one of those cases is this observation here of the photoelectric effect. So, what we're going to do is look at both tracks of observations here./nAnd we are going to see how these observations made it such that it was impossible to explain how an atom held together, how an electron and a nucleus held together within the classical way of thinking, within the Newtonian mechanics, the mechanics that you are going to be looking at this semester in 8.01./nYou cannot use that mechanics to understand how this electron and the nucleus stay together. You cannot use that mechanics to understand how two atoms are bound together. We need a new way of thinking./nAnd it is these two tracks of observations that led to the discovery, in a sense, of this new kind of mechanics that we are going to be talking about. OK, so let's start on one of these tracks. And that track of seeing that the atom is not the most basic constituent to matter./nAnd the first observation was done by this gentleman, J.J. Thomas. It was the discovery of the electron. OK, so I am going to need the lights on again. All right. What J.J. Thomas was interested in doing was understanding what deep discharges were made of so he had a glass tube that was evacuated./nAnd in it he had what we're going to call here a cathode. And he had an anode. And, as I said, a glass tube pumps out the air and then he fills it up with hydrogen, H2. And what he does is he puts a large negative potential on this cathode./nAnd on the anode he puts a large positive potential, and he cranks up the potential difference here. And he keeps cranking it up until at some point the gas begins to glow. And it is at that point that this discharge here is ignited./nAnd this is kind of plasma. And he wanted to understand what is in this plasma. He was just curious. He wanted to know. And so what he does is he pokes a hole here in this anode. There's a hole./nAnd he lets out a little of this discharge. And he lets it out. And my chalk is breaking. He lets it out. And way back here he has some kind of a screen, a phosphor screen so that not only does this discharge here kind of glow as it's moving along, but when it hits the phosphor screen it lights up./nAnd so that's nice. But then what he does is he takes two parallel plates and puts them above and below this luminous beam, and there is a positive charge on one of these and a negative charge on the other./nAnd, low and behold, when he increases this potential difference, this delta V what happens is that this luminous beam, some of that luminous beam is actually deflected a little bit. And so now there is another very bright spot./nAnd he can measure this deflection. And we are going to call it delta X. Now, since some of this luminous beam was deflected toward a positively charged plate, what kind of particles did he decide were in this luminous beam? Negative particles because they're attracted to the positively charged plate./nSo, he called this deflection delta X. We will call it delta X sub minus. Now, he knew enough about electromagnetism at that time to realize that the amount of that deflection has to be directly proportional to how much charge was on the negatively charged particle./nAnd I am going to call that e sub minus. Because the more charge the easier it would be to deflect it. And he recognized that the amount of deflection has to be inversely proportional to the mass of that negatively charged particle./nBecause, after all, the more mass of that was the more difficult it was going to be to deflect it. And then what he did is he cranked up delta V as much as he could. And here I am taking a little liberty with the story./nI'm telling essentially the essence of the experiment, but it is a little more complicated than what it is I am going to tell you right here. But he cranked that up. And when he did, he realized that there actually were some other particles that were being deflected toward the negatively charged plate just a little bit./nAll right? Not a lot. Just a little bit. And, again, he could measure that deflection. And he called that, or we are going to call that delta X sub plus. These have got to be positively charged particles because they are attracted to the negatively charged plate./nAnd, again, he realized that delta X sub plus is proportional to a charge on that positively charged particle and inversely proportional to the mass of that positively charged particle. All right. But now here comes his thinking./nWhat he guessed is that these positively charged particles were H+, a hydrogen ion. How did he know that? Well, this was a guess. However, he did know that in this plasma, this discharge that there were hydrogen atoms./nAnd how he knew that is something we're going to talk about in a few days. But he knew that. He also knew H here, these hydrogen atoms that are produced in the plasma, somehow the plasma breaks the H2 bond, these hydrogen atoms were neutral./nAnd so he said, well, if it's a positively charged particle, well, gee, it must be that something was removed from the hydrogen atom to make it positively charged. And that something must be this negatively charged particle that I'm observing because I knew that originally the hydrogen atom has to be neutral./nSo, therefore, I am going to guess that the magnitude of the charge on the negatively charged particle is equal to the magnitude of the charge on that positively charged particle. And if that it is the case then I can take a ratio here of the deflection of the negatively charged particle to the deflection on the positively charged particle./nAnd, since these two are equal, I am guessing that, well, then this ratio has to just be equal to the mass of that positively charged hydrogen atom to the mass of that negatively charged particle. All right? And now here is the important point./nThe important point is that no matter how he made these measurements, no matter how he did that, the deflection for that negatively charged particle was much, much, much larger than the deflection for that positively charged particle./nThat then meant that the mass of this positively charged particle, which he guessed to be a hydrogen atom, must be much, much larger than the mass of the negatively charged particle. He also knew at that time that a hydrogen atom was the least massive atom, but here is an experiment that showed that there was a particle that was less massive than a hydrogen atom./nHey. But up until then it was the atom is the most basic constituent of matter. You cannot chop it up anymore. But here was the evidence that there was a particle less massive than the hydrogen atom./nEventually it is called an electron. But this is the first evidence here that the atom wasn't the most basic constituent of matter. Now, it actually took another ten years with the Millikan oil drop experiment to actually measure this ratio correctly and to determine the mass of the electron./nWe won't go into that. But this ratio here, you probably all know, the mass of the electron is about 836 times that of the mass of the hydrogen atom or hydrogen ion.
Tags //
chemical science atomic theary
Added: April 16, 2009, 10:18 pm
Runtime: 2519.20 | Views: 24367 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science - Wavelike Properties of Radiation - Lec 3
Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 3/nTopics covered:
/nWavelike Properties of Radiation/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 3/nAll right. So by last Friday we discovered the electron, discovered the nucleus. And the problem then was how to describe the structure of the atom. They knew there was an electron, they knew there was a nucleus, but exactly how did the electron and the nucleus hang together? And we talked about how the scientists at that time proposed a classical model where the interaction between the electron and the nucleus was, of course, the Coulomb interaction, but where the equations of motion were Newton's equations of motion to describe this electron going around the nucleus, F = ma./nAnd, although we didn't show it, what we said was that if we used that force field, the Coulomb force, coupled with Newton's equations of motion. And, actually, you also have to couple them with some classical electromagnetism, which I may not have said but which isn't important./nBut if you use those classical ideas to describe how that electron goes around that nucleus, well, you would find that in 10-10 seconds that electron would be on top of the nucleus. And you would no longer have what we know to be the structure of the atom in the sense that you would no longer have some volume where the diameter of that volume is on the order of an angstrom or so./nThe bottom line is that classical ideas, classical mechanics and classical electromagnetism just totally fail to explain the structure of the atom. And that was the conundrum that the scientists faced in 1911./nThis was quite a big problem for the scientific community and was so for about 10, 12, 13 years. And, of course, what fails are the classical equations of motion, Newton's equations. A new kind of mechanics is going to have to be invented in order to understand how that atom is bound or how the electron and the nucleus are bond, how it's stable./nBut now, historically, the actual clues for why the electron didn't collapse into the nucleus. Those clues actually came from a very different area of discussion, and that area of discussion is this wave particle duality of light and matter./nIt was certainly long believed that matter, with its particle-like behavior, was distinct from light, which was this kind of transmission of energy through space. But in the late 1800s and early 1900s, there began to be made some observations that seemed to suggest that well, you know, maybe this boundary between matter and its particle-like behavior and light and its wave-like behavior wasn't so rigid after all./nAnd, in fact, what we're going to see is that radiation or light exhibits both wave-like behavior and particle-like behavior. And it depends on the kind of experiment that you do which one of those properties you see, and that consequently matter also exhibits both particle-like behavior and wave-like behavior./nAnd, again, it depends on the particular experiment that you do as to which one of those properties you actually observe. What we are going to do right now is we're actually going to set aside the discussion of the structure of the atom, how the electron and the nucleus are bound together, how in the world do they remain stable? We are going to set that discussion aside, and we are not going to pick it up until next Monday./nAnd the reason for it is because in order to proceed with that discussion, we actually have to go through this other set of observations, this discussion about the wave particle duality of light and matter in order to get the clues, in order for us to make progress about what next big leap we've got to make in order to talk about the structure of the atom./nWe are going to change subjects, or it's going to look like we're changing subjects, but we're going to use the results of our discussions in the next three days to come back to talk about the structure of the atom./nThen the first thing we've got to talk about is we're going to talk about light and we're going to talk about the wave-like nature to radiation. And since that is really probably most intuitive, let's do that./nProperties of waves. Well, what are waves? Well, you are familiar with that. Waves are a periodic variation of some quantity. In the case of water waves, we have the periodic variation of the height of water./nAt some points in space here, the height of the water is high, at some point the height of the water is low and there is some average level here. A sound wave. Well, a sound wave is a periodic variation of the density of air./nAt some points in space the air is very dense, at other points in space the air is not so dense, and then there is an average level here. Well, what we're going to do is we're going to set this average level here to a zero./nAnd then, consequently, our waves are going to have a positive amplitude that is measured from this zero level up. That's a positive amplitude. And measured from zero level down, that's our negative amplitude./nThese waves are going to have positive and negative amplitude. That is going to be very important in how they actually behave. Now, what we're going to do, oh, so what is light? Well, light is a periodic variation of an electric field./nAnd that is what I plot here. Electric field versus distance. And you can see it is varying in intensity. But what exactly is an electric field? Well, let's just think about that for a moment. Suppose I take two parallel plates, here is one and here is another, and I am going to put a negative potential on that top plate and a positive potential on the bottom plate./nAnd what is operating then between this negatively charged plate and the positively charged plate is the Coulomb interaction. And the electric field then is the space through which that Coulomb force operates./nSo, that electric field here is this space through which this Coulomb force is operating. And, by convention, we are going to say that it is operating here in this orientation. In other words, if I put a positive charge in between these two plates, in this electric field, this space through which the Coulomb force is operating, well, what's going to happen is that this positive charge is going to drift to the negatively charged plate./nBut if I turn the geometry around. If I put the negatively charged plate on the bottom using this coordinate system. And I now put that positive charge in that electric field. It's going to drift to the negatively charged plate again, but it's going to move in this coordinate system down./nSo, this electric field has not only magnitude, because you can imagine the larger the potential difference between these two plates the larger the magnitude of the electric field. But that electric field also has direction./nIt is pointed in one way or the other. And that is what represented here on my diagram of the electric field versus distance. You can see that right here the electric field, the magnitude of it starts out small, it increases, continues to increase until we get a maximum, and then it starts getting smaller./nIt gets smaller and goes all the way to zero at which point then it turns around and the magnitude begins to increase in the opposite direction. And, again, it becomes a maximum in the opposite direction and then turns around and goes to zero and continues./nSo, it's a periodic variation here of an electric field. And so what that means is that if we put some charge, say, at this point in space, it will be pulled one way. And if we put it at this point in space, it will be pulled yet another way./nAnd if we put it right here at zero, it's not going anywhere. Now, what I've shown you here is a periodic variation of an electric field. It is also the case that whenever we have an electric field, we also have a magnetic field that is actually perpendicular to this electric field here./nBut since that magnetic field is going to have all the same characteristics as the electric field, from our point of discussion here, I am not going to talk about it, but you are going to see this a lot next semester in 8.02./nSo, we are just going to characterize here the electric field. And the way we're going to characterize it is to put a functional form to it. I am plotting the electric field here as a function of X./nAnd the functional form that we are going to use to characterize it is Acos(2pX/?), a cosine function. Now, what I want you to notice is that this field oscillates between a positive amplitude A and a negative amplitude A, or a minus A./nThis coefficient right out in front, right here, that coefficient physically is the maximum amplitude. So, if you were to be given a waveform that has a number out here in front of a cosine X, that number, immediately the physical significance of it is that it's the maximum amplitude./nThe other parameter, besides the amplitude here, the maximum amplitude that we use to characterize this cosine function is the wavelength. The wavelength is the distance between two successive maxima or two successive minima./nAnd that wavelength here comes in the argument of that cosine function. Again, if you were to be given a form that had a number times cosine times a number times X, well, that number is equal to 2p/?./nAnd so almost by inspection you can figure out what the wavelength is just from the functional form of that cosine function. And because the argument is 2pX/?, well, you can easily see that you get the maximum amplitude A here whenever X is an integral multiple of lambda./nWhen X is ?, 2?, 3? or -?, -2? or 0. Most of that, I think, you're familiar with. But not only is light, or formally electromagnetic radiation, simply a periodic variation of the electric or magnetic field, but light is also a period variation in time./nThat is light propagates, it moves. For example, here is a cosine functional form at some snapshot in time, T = 0. And I put a star here on the maximum of one of these maxima. Now, what happens is that this wave moves./nIt propagates. And the time it takes that wave to move one wavelength, just like it did in that very short clip -- The time it takes to move one wavelength so that this maxima that was here is now there is what we call a period./nOne period is the time it takes the wave to move one wavelength. And we can also characterize the period by the frequency of the wave. That frequency is new here and the period is one over nu. And the frequency then is the number of cycles per second./nIn other words, if I were sitting right here at X = 0 and I am just watching the wave come by me, the frequency is the number of times that a maxima passes by me per second or the number of times a minima passes by me per second./nThat is the frequency. I will make that a little bit more obvious in just a moment. Frequency, I said, is the number of cycles per second. But the unit that we use to convey frequency in something called the hertz, hz./nAnd formally it is just inverse seconds. We drop the number of cycles, but the number of cycles in that unit is implied. Now suppose the following. I said that this electric field has magnitude and it also has direction./nSuppose I take an electric field or an electromagnetic radiation that has a frequency of 1 hz, one cycle per second. And right here at X = 0, somehow I pin an electron right there. It cannot move anywhere./nIt's just stuck. What is going to happen to that electron as this radiation of 1 hz passes by? Well, what's going to happen is that that electron, since it's starting at the top, is going to be pulled down./nAnd then it is going to be pushed back up to its original position every one second because this frequency here is 1 hz and because this electric field has both magnitude and it has direction. Now we're going to let this electric field go by, the electron gets pushed down and pulled back up once every second./nHopefully that makes the idea of frequency a little bit more real to you. Not only do we have this periodic variation in time, but we also have the wave propagate here in space. That wave moves this way or this way or this way./nAnd so what we want to know is the speed of that propagation. Now, speed is always distance traveled over the time elapsed. And what we have already seen is that this wave will move by one wavelength in the time period of a period./nThat is we already saw that this wave will move here one wavelength, from here to here, in the time period of a period or one over new. That's the time elapsed. So, the speed of this propagation, the speed with which it's moving is the distance traveled, which is lambda, divided by the time elapsed, which is one over nu./nAnd, therefore, the speed of that propagation is lambda times nu. These are the important concepts here. We have the speed of the propagation, lambda times nu, we characterized our wave in terms of amplitudes, in terms of wavelengths and in terms of frequency./nThose are the quantities that are important that you really do have to understand very well. Now, I think that you are all familiar with the fact that all electromagnetic radiation has a constant speed./nThat is the wavelength of electromagnetic radiation times the frequency is always equal to this number. It's about 3 x 108 meters per second. And we abbreviate it C, the speed of light. No matter what frequency you have of radiation, the corresponding wavelength is such that the wavelength times the frequency is this constant, is this value of C./nAnd, of course, it is the different frequencies or the different wavelengths of electromagnetic radiation that gives it its different characters. Even though it all has the same speed of propagation./nAnd those different kinds of properties, so to speak, are this spectrum of electromagnetic radiation. So, electromagnetic radiation is an infinitely wide spectrum. At very long wavelengths we have what are known as radio waves./nAt very short wavelengths we have what are known as gamma rays or cosmic rays. The long wavelengths, the radio waves are going to have a relatively low frequency. The short wavelengths are going to have a relatively high frequency./nWhy? Because the product of lambda times new always has to be C. Well, we're not going to go very much in detail here, except maybe to tell you the following. See this microwave range here? Well, molecules, when they absorb microwave radiation they rotate./nSee the infrared radiation? When molecules absorb infrared radiation they vibrate. See the visible and ultraviolet range? When molecules absorb visible or UV radiation they put an electron into a higher energy state./nAnd often times, once you do that, of course the electron wants to relax to a lower energy state, and so it relaxes by emitting a photon. And that's how you see fluorescents or phosphorescent. But it's usually a result of the absorption of visible or UV radiation./nAlthough, it is also possible for a molecule to absorb some x-ray radiation and see that kind of fluorescence, too. And we will talk about it. But a little bit later on we're going to talk about molecules absorbing x-ray radiation and kicking out an electron./nAnd we are going to use that to figure out how strongly bound electrons are in atoms or how strongly bound they are in molecules. But that is all I will say about that right now. What you are responsible for is -- You are responsible in knowing that microwaves have longer wavelengths than gamma rays or cosmic rays./nYou are responsible for knowing the relative wavelengths here of these different kinds of radiation. Every MIT student should know that. Of course, there is a very narrow range here of visible radiation that our eye is sensitive to./nAt the very long wavelengths is red. At the very short wavelengths is blue and purple. Again, you need to know that red has a longer wavelength than blue or purple. What I have done right now is really just to tell you that light is an electromagnetic radiation characterized at the wave./nI put a functional form to it, cosine, characterized it by frequency, wavelength. We talked about speed of propagation. What I haven't done yet is I haven't proved to you that light is, in fact, or light behaves like a wave./nAnd that is what we are going to do now. And the experiment we are going to do is the same experiment that a gentleman called Young did in the lat 1800s that seemed to really demonstrate, without a question, that light is a wave or light behaves like a wave./nWe are going to do what's called the two-slit experiment. And in this experiment, we are going to take radiation of a single wavelength, so we're going to make the radiation monochromatic. And that wavelength that we are going to use is 6,330 angstroms or 633 nanometers./nAnd we are going to put in front of that source, we are going to put a thin piece of metal, or it could be any material, but we are going to pock two holes in it. We're going to make two little slits./nAnd naively what you might expect is, if you have a screen back here that kind of images this radiation -- What you might expect is that the spots on the screen right directly opposite these two slits, well, these are the two spots that are going to light up on the screen./nThat is where you're going to see the image because, after all, light travels in straight lines. That's where you should see those two spots. If the slits here are 0.02 inches from each other, these two spots ought to be 0.02 inches separated from each other./nBut, of course, when you do that experiment, and Christine is actually going to do that experiment right now for us, I think, there it is, on the side board. You can sort of see it. She is holding it./nWell, what you can see here is that we don't see just two bright spots. But what we see is a bunch of spots here. The brightest one happens to be right in the center of these two slits. And then there is darkness and then there is a bright spot and darkness, and a bright spot, etc./nWe see lots of different bright spots on the screen, not just two directly opposite the openings of the slits. And this is just then a cartoon of approximately what it is we see in real life. Christine is up there in the projection booth holding a helium neon laser behind these two slits separated by 0.02 inches./nWell, what's going on here? Can we understand what the origin is of these lots of different bright spots in this two-slit experiment? Actually, if we were to measure that, the distance here should be about 3 cm between those bright spots./nWell, what's going on? Well, what's going on is this. Waves have the property called superposition. That is if I take one wave, but then I take a second wave and I put that second wave in the same space, the actual same space as the first wave, and I arrange the two waves such that the maximum of both waves or the minimum of both waves is at the same position, well, the property of waves is that these two waves add up./nThey superimpose. They superimpose to make a wave that now has the amplitude of twice the amplitude of each of those waves. And that is the condition that we call constructive interference, but we have to have the two waves at the same place in space and the two maxima have to be in the exact same place in space./nBut conversely we can also take the wave and bring in another wave, but we can move that other wave over such that the maximum of one of the waves is at the same place in space as the minimum of the other wave./nIn this case, these two waves are out of phase. And when we add them up there will be nothing. This is destructive interference. Why? Well, because we have positive amplitudes and negative amplitudes./nThey cancel to give us nothing. Destructive interference. And there is a website here at the University of Colorado that lets you take two waves and superimpose them. I need to play with it. What I am going to do is I am going to make it so that these two waves have the same frequency or the same wavelength and the same amplitude./nWhat I am doing here is I am adding this wave, I am adding this wave right here to this wave, and the result is shown here. And what you cannot see is that the amplitude down here, that amplitude is twice that of these two./nThere is a two there. But, of course, what I can do is I can move this wave over such that the two waves are now at the same place in space, sort of, where the maximum and the minima are at the same place in space and exactly cancel them./nAnd I am not having such a great time doing this here, but I know you can do it because I have done it before. And you can see that the resulting amplitude is zero. And, of course, then you can go home and you can play all you want with this, make all kinds of different waveforms./nI am trying to change the amplitude here, which I have done before, but I cannot right now. You can do whatever waveform you want to. You get the idea here with superposition. So, that's a characteristic of waves./nThey have positive and negative amplitudes. They add and they cancel depending on the relative positions in space. But now let's talk a little bit more about this pattern that we saw in the two-slit experiment./nThis kind of row of bright spots. And, to talk about it, what we are going to do is we're going to use water waves to try to explain it. Here is a picture of the beach. Here is the water, here is the sand, and here is where I wanted to be all weekend./nAnd the waves are coming in to the beach. These straight blue lines are the crests of the waves rolling into the beach. And suppose I get ambitious and I erect a barrier right here at the shore, a sand barrier, but for whatever perverse reason I poke two holes in that sand barrier./nWell, what is going to happen as the waves roll up? Well, what is going to happen is that a little bit of the wave here, this is kind of like a pinhole, is going to leak through. When it leaks through, it is going to spread out equally in all directions./nAnd so the wave front is going to look like this semicircle here. That is the wave crest. It is going to look like a semicircle. And that is going to propagate out. And when it propagates out to a distance of 2?, well, then another wave has snuck in here through this hole and it propagates out./nAgain, the distance between these two semicircles is lambda, is the wavelength, because these are the maxima of the two waves. And, as time goes on, that propagates further and another wave sneaks through that whole and another wave sneaks through and the whole thing propagates./nMeanwhile, while that is happening, there is also a part of the wave sneaking through this hole and it emanates out in all directions and propagates out in all directions. And let me, for the purpose of talking about this, call this slit slit 1./nAll the green waves are the waves that came through slit 1. And I am going to call this slit 2. And all the blue waves are the waves that came out slit 2. And, again, the distance between any of these two crests is the wavelength./nAnd the wavelength is the same for the waves coming from slit 1 and slit 2. Now what I want you to do is I want you look at this point right here. See that point? Well, right at that point, what we have is we've got the wave crest, the wave maximum from slit 2 at the same point in space as the wave maxima from slit 1./nIf we've got two maxima at the same point in space, hey, we've got constructive interference right there, because those amplitudes are going to add. Look at this point. Well, again, we've got the wave maxima from this blue wave coming through slit 2 at the same point in space as the wave maxima from the wave coming from slit 1./nAgain, this is a point of constructive interference. And we can keep going. Again, we have two maxima right here, a point of constructive interference. And, you know what, everywhere along this line we are going to have constructive interference./nWe are going to have a resultant wave, a water wave that is going to be twice as high as each of the individual waves. Look at this. What I want you to notice here, for this point, the wave that is constructively interfering, that has traveled from the slit a distance R2, because this is slit 2./nBut the distance from here to here is 4?. It is 1?, 2?, 3?, 4?, right? The radius R2 of this circle is 4?. And it is interfering with this wave crest. And the distance that that wave traveled from slit 1, I am going to call R1, and that is equal to 3?, 1?, 2?, 3?./nThis interference here is between this wave that has traveled out a distance, 4?, and this wave that has traveled out a distance, 3?. And the difference in the distance traveled by those two waves that are constructively interfering is 4? - 3? = 1?./nIs there a question over here? Yes? I think I am coming to that. That was a snapshot of the next slide. Sorry. Yes? Because we are treating these as regular waves, ordered waves. Real waves on an ocean are not like that./nAnd then you won't see this diffraction pattern that I am erecting here. But, if you had pretty regular waves coming in, in principle you could see it. And I am going to show you, in a tank, some water waves that do just this./nNow I want you to look at this point right here. Right here we have a point of constructive interference because we have two maxima at the same point in space. And at this point we've got constructive interference./nSo, everywhere along this line here we are going to have constructive interference. And now I want you to look at the difference in the distance of the waves that yield this constructive interference along this line./nI want you to look at this green wave that is constructively interfering with this blue wave. This green wave has traveled out a distance R1 or 2?, and it is interfering with this blue wave here that has traveled out a distance 4?, R2 = 4?./nSo, the difference in the distance traveled for all of these points that lead to constructive interference, the difference in the distance traveled here is R2 ñ R1 or 4? - 2? = 2?. Does that agree with the snapshot in your picture? Yes./nI just didn't show you the other one. Now I want you to look here. Here is a point of constructive interference. Here is another point of constructive interference. Everywhere along this line we are going to have constructive interference./nAnd, if we check out what the difference in the distance traveled is between the waves that are constructively interfering there, you are going to see that R2 ñ R1 = 0. Now, what you would predict is we would have along this angle some very bright spots, along this angle some very bright spots./nAnd along this angle some very bright spots. And you also can see that this is going to be symmetric about the center, so you would have bright spots here, bright spots there. Well, let's look at this in real life in a water tank where we have plain waves coming into a barrier and then we have two little slits right there and right there./nAnd what you can see is that these bright semicircles are, in fact, the crest of the waves. But what I want you to see is right here -- This bright row, here is a bright row, here is a bright row. And in between there is kind of just a muddy diffuse pattern./nWell, this diffuse pattern is nothing. This is a bright row. You get the idea. You are going to have an angle which there is going to be constructive interference, several angles of which there is going to be constructive interference./nAnd in between those places where there is constructive interference there is destructive interference and you are not going to have any light. How does that relate to what we saw in the two-slit diffraction experiment? Along this line we have waves that have constructively interfered, and they constructively interfere so that on the screen right there you have a bright spot./nAnd along this line, the difference in the distance traveled by the waves that constructively interfere is 1?. And then we've got another row or another line, points of constructive interference. That is going to image as a bright spot./nAnd if you analyze that, the difference in the distance traveled by these two waves is 2?. And then we're going to have another bright spot here. For all the constructive interference along this line, the difference in the distance traveled is 0./nAnd, of course, I said before this was symmetric around the center. And so this is what gives rise to the different bright spots on the screen when we did the two-slit experiment. Bright spot. Dark spot./nBright spot. Dark spot. The bright spots are constructive interference. The dark spots here are destructive interference. Now, let me just tell you that the general condition for having these bright spots -- The general condition that has to obtain is that the difference in the distance traveled has to be equal to N, an integer, times lambda./nThis bright spot, the difference in the distance traveled, N = 0. We call that the zero order spot. This bright spot, the difference in the distance traveled is lambda, or N? where N = 1, first order interference feature./nHere, the difference in the distance traveled is 2?, N2, called the second order interference features. And the condition for that is this, R2 - R1 = N?. There is also a condition for destructive interference, which I ask you to think about, and we will talk just briefly about its origin next time./nAll right. See you on Wednesday.
Tags //
Chemical Science Wavelike Properties Radiation
Added: April 16, 2009, 10:19 pm
Runtime: 2768.53 | Views: 14160 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science - Particle-like Nature of Light - Lecture 4
Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 4/nTopics covered:
/nParticle-like Nature of Light/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 4/nAll right. Let's just remind ourselves for a moment where we were, and that is that we were talking about the structure of the atom. And we talked about how classical physics, the classical mechanics, classical electromagnetism failed to explain how the electron and the nucleus hung together./nAnd I said that the clues about how to solve that conundrum actually came from a different area of discussion, and that is this wave particle duality. And so remember that I said we are going to put aside that discussion of the structure of the atom all the way until next Monday. Pardon? No class Monday? We're going to put it aside all the way until next Wednesday./nThank you. [LAUGHTER] You sound surprised? You're not. It's a student holiday on Monday. And we're going to talk about the wave particle duality of light and matter, get clues from that area of discussion, and we're going to apply those clues then to solving the structure of the atom next Wednesday.,/nNow, we started on this discussion by talking about the wave-like nature of radiation. And to illustrate that, we did this two-slit experiment where we saw an interference pattern. And we talked about how that interference pattern arose because of the property of superposition of waves. That is if you have waves in the two same points in space their amplitude superpose or they add./nAnd because some of those amplitudes are positive and some are negative, depending on the relative phase of the waves, you have constructive or you have destructive interference. And specifically what we were trying to understand is, in the two-slit experiment, why we had this line of bright spots, dark spots, bright spots, dark spots./nAnd we analyzed it by drawing these semicircles which represent the wave front kind of sneaking through this little pinhole here, this slit, emanating equally in all directions. These semicircles here represent the crest of the wave. The distance here between these crests is 1?, is one wavelength. And can we dim the lights in the front here?/nIf you closely, what we discovered is that all points along this line constructively interfere. That is we have waves that are at the same place in space and the maxima and the minima are in the same place in space, and so that's going to lead to a very bright spot here on the screen. The amplitude is going to be twice as high as it was in each of the individual waves./nAnd we get this very bright spot. And we realize that along this line the difference in the distance traveled by the two waves that are constructively interfering was 1?. And then we did so for this line here. And we discovered that all along this line we had these two waves in phase./nAll along this line we had constructive interference which, of course, imaged as another bright spot. And when we analyzed it, we found that the difference in the distance traveled by the two waves was 2?. And likewise here. All along this line we had constructive interference imaged as a bright spot. And we recognize that in this case the difference in the distance traveled by the two waves was 0?./nAnd given that pattern, we then concluded that there was a general condition for constructive interference. That is if you had maximum constructive interference, the general condition that had to apply was this, that the difference in the distance traveled by the two waves was an integral multiple of the wavelength where this integer N could be 0 or 1 or 2 or 3 or 4./nAnd it's actually symmetric here along the center of the two slits. So, you would see the same kind of interference pattern up here. And so we call this interference feature right here, we often call it the zero-order interference feature. We call this one, when N is equal to 1 the first-order. We call this one the second-order interference feature./nAnd in between the very bright spots on that screen, what we have are dark spots here, here and here. And what I am going to ask you to do in recitation section, actually next Tuesday, is to look at what condition has to apply in order to have these dark spots which result from destructive interference./nAnd, of course, when you analyze that you're going to see, say right here, the crest, the maximum of one wave at the same point in space as the minimum of the other wave. And you get maximum destructive interference everywhere along that line. And what you will do in recitation next week is actually to figure out what the condition is for destructive interference. And that is going to be N + Ω?./nSo, it is this observation of these interference phenomena that are characteristics of the wave-like nature of anything. In this case, the wave-like nature of light, of radiation. On Friday, what we are going to do is we're going to see this same sort of interference phenomena, a property of waves, be observed from particles, from electrons. This diagram you are going to see once again on Friday. And we will use that to demonstrate the wave-like nature of particles, electrons. That is our evidence for the wave-like nature of light./nNow what we are going to do is we're going to talk about the other behavior of light, and that is the particle light behavior of radiation. And I forgot to get out my notes. What is that evidence? Well, soon after Thompson's discovery the electron there were some observations being made of something called the photoelectric effect./nAnd this was very curious. The photoelectric effect is simply that you have some metal here and you shine some light on that metal. And what happens is that an electron is ejected. Metal. Light coming in. Electron comes out./nBut the frequency of this light that is coming in, this frequency nu, we talked about frequency the other day, has to be greater than or equal to some threshold frequency, some threshold frequency that I am going to call ?0. In other words, if I come in with radiation here that has got a frequency that is less than ?0, well, then no electrons come off of the metal./nMaybe we could raise the screen here for the moment. Well, another way to kind of plot that observation is to just plot number of electrons versus the frequency of the radiation./nAnd so if you're at low frequency there are going to be no electrons that come off, but then when you get to some frequency ?0 all of a sudden electrons are going to come off. And the number of electrons that come off is going to remain constant as you increase the frequency of the light. And typically this frequency of the light that causes these electrons to be emitted is in the ultraviolet range./nWell, this was a curious observation in the late 1800s, very early 1900s. And scientists just started to measure everything about these electrons they possibly could measure because they just didn't understand the effect. And one of the things that they measured is the kinetic energy of the electrons./nHere I am going to plot kinetic energy, KE. And they measure the kinetic energy of the electrons as the function of the frequency of the light. Again, at low frequencies there is no kinetic energy because there are no electrons. But then here at some frequency v0 all of a sudden electrons come out. And these are points just representing the individual measurements./nLow and behold, as you increase the frequency above v0 the kinetic energy increased. It increased and looked directly proportional. The kinetic energy looked directly proportional to the frequency of the light. Well, let me tell you, that was a big mystery as far as classical physical ideas were concerned. That was a big mystery./nBecause, in the classical physics that was understood at that time, the kinetic energy of the electrons, KE as a function of the frequency of light, well, that classical physics would predict that that kinetic energy were independent of the frequency of the light. There was nothing in the known classical physics, classical electromagnetism that would allow the frequency of the light to be related in any way to the kinetic energy of the electrons kicked off./nThere was no reason for why bluer light, which has a higher frequency, would eject electrons and redder light, which has a lower frequency would not eject the electron. And classical physics also predicted that the kinetic energy of the electrons should be dependent on the intensity of the light./nI am going to call it i. In kind of general this sort of dependence. That is the brighter the light, the more kinetic energy these electrons ought to be kicked out with. In other words, the brighter the light the more energy you were putting into that metal. And, therefore, the electrons should be kicked out with more energy./nThat's what classical physics was predicting. But, go in the lab and you do the measurement, the measurement showed that the kinetic energy was independent of these intensities of light. This is the experiment. It had nothing to do with the intensity of the light./nThe kinetic energy remained the same no matter how bright that light was, not matter how much energy you were sticking into the system. Now, as you put more and more energy or as you put more and more intensity, what changed was the number of electrons that came off but not their kinetic energy. So, this was another conundrum here in terms of being able to explain it with the known classical physics at that time./nThese data were around for a few years before Einstein took a look at it. And he looked at these plots of the kinetic energy versus the frequency of the light. He looked at it, say, this is the data for metal B./nHere is the data for metal A. In all cases, it kind of looked like it was linear dependent on it. And the only thing that was seemingly different, for the different metals, was the threshold frequency here. What Einstein did, a real leap here of intuition, was he went and he fit a straight line to this data./nWell, he did a better job fitting a straight line than I did. He fit a straight line here. y = mx + b, no problem, where kinetic energy is y and x is v, right? He looked at that and calculated the slope. And he looked at it and he looked at it./nAnd he goes finally, very interesting, because what was so interesting here was the value of the slow, the value of m. The value of this slope here was equal to 6.626 x 10-34 joule seconds./nNo matter what metal he looked at, the value of the slope was 6.626 x 10-34 joule seconds. So what you say? Well, it was very interesting to Einstein, because just a few years before there was a gentleman who was analyzing what's called black-body radiation data./nLet me just explain this a little bit to you, but you're not responsible for it. What is a black-body? Well, let's just, for a simple example, think about the burner on your electric stove. We will consider that to be a black-body. What you know is that when you turn up the voltage the temperature starts going up and at some point the temperature gets high enough such that the burner glows a little bit dull red./nAnd then if you turn it up some more it gets hotter, the burner glows a little bit redder. That's the black-body radiation. If you turn it up some more the burner glows orange. Frequency going up. If you turn it up some more, and you better not do this, the burner starts glowing yellow. And then, if you could, and you probably cannot turn it up some more, it ultimately is white. All frequencies./nNow, what scientists had been doing is they had been analyzing the intensity of that radiation from a black-body as a function of the frequency. And they did it for lots of different temperatures. This is our black-body radiation. I am plotting the intensity here./nAnd so they dispersed the radiation, they analyzed it as a function of frequency, and what they saw was a curve that looked kind of like this. And this temperature here, we will call it T1, that was for some temperature T1, a low temperature. This isn't in your notes because you're not responsible for this. I'm just trying to make the importance here of this slope, or I'm just trying to illustrate the importance of this value for the slope in the photoelectric experiment./nAnd then at a higher temperature here, T2, the intensity got bigger, but also the maximum shifted to higher frequency. And at temperature T3, here now T3 is greater than T2 and greater than T1, frequency shifts even to a higher frequency./nThat was the observation. This is dull red, red, orange, etc. Well, Planck, along with a lot of other people, was trying to understand those curves. And he came up with a model. And the model said that materials, these black-bodies, had oscillators in them. And these oscillators were emitting radiation./nThese oscillators were responsible for giving off this radiation. And he also added another twist to those oscillators in that those oscillators were quantize, that they could only emit discrete packets of energy. And using that basic idea and something called statistical mechanics he was able to calculate the shapes of these curves./nA lot of his calculation. And so this green here is going to be a calculated curve here for T = 1, a calculated curve here for T = 2, a calculated curve here for T + 3. He got the shape right, but he didn't get the magnitude right. And he said how do I get the magnitude right?/nWell, what he realized is that in that formulation what he had to do was multiply the frequency of the oscillators by this constant m or this constant that is called h, Planck's constant. Where does Planck's constant come from? From this. Hey, that's it. It is, in a sense, a fitting constant./nThere isn't any derivation of Planck's constant. You cannot sit down and derive Planck's constant. It is our observation of the way nature works. So, that is where Planck's constant comes from. And so you can imagine Einstein's surprise when he analyzed these photoelectron data. And, low and behold, out from the data comes the same constant that Planck had found./nAnd Einstein realized that there must be something really very fundamental about this h, about what is now known as Planck's constant. So, he pursued. And what he did then was he just wrote down the equations here for that straight line./nThat's kinetic energy is equal to nu, that is my x, the slope is h, and he found that the intercept here was -hv0. So, this will be then plus the intercept, or -hv0. That was the equation of the line he fitted through the data./nNow, he also realized he has energy units on this side so he better have energy units on this side. If this is a frequency then h must have the unit such that hv0, this has got to be energy. And since this is the frequency of the light coming in, this energy E must be the energy of the incident light./nAnd here is where this equation E = hv comes from. This is it. This is where this equation comes from. What it is telling you is that the energy of the light is proportional to the frequency. This was the first time that there was any indication that the energy of the light had anything to do with the frequency of the light./nThe very first time. And what E = hv ended up being thought of is as a particle of energy, as a packet of energy, as a quantum of energy, eventually going to be called a photon./nThe photon, this particle or packet of energy is given by its frequency times this constant, this natural constant h, Planck's constant. You could have here any frequency of light you wanted, but the energy of that light only comes in chunks given by this quantization constant h times that frequency./nI will explain that a little more in just a moment. Well, likewise, this hv0 here, that better be an energy also. And so what that hv0 is, is the threshold energy. Since v0 was a threshold frequency hv0 better be the threshold energy./nAnd let's try to understand that in terms of an energy level diagram. I am going to plot here energy. This electron that is bound to the metal, before we shine any light on it, I am going to let its energy level be represented here by this line. This is the electron bound to the metal way down here./nAnd what we know now is that it takes some energy, hv0, to rip that electron apart, to pull it off. And so I am going to draw another energy level up here which is going to represent the energy of the electron free from the metal. So, I will call it electron free. And the amount of energy that we have to put in to get it out is this threshold energy, hv0./nThis energy here is like an ionization potential, which you are familiar with. The energy required to pull an electron off an atom or a molecule, the ionization potential. Well, this is like an ionization potential. It really is the ionization potential, except since it's coming off of a metal historically we call it something else./nIt's called the work function. And we give it often the symptom phi. But F and hv0, they are the same thing, the energy required to rip the electron off. And so what we know is that the packet of energy that you send in here has to be at least this amount./nIn other words, if you come in with a photon and the photon has this much energy, Ei = h0, you can ripe the electron off, but you have to have at least this. Now, you can come in with a photon that has more energy than that, Ei, from here to here./nBut if you do then the rest of this energy here goes to the kinetic energy of the electron. So, if you come in with exactly the energy, the electron is ripped off but it doesn't move away from the metal. If you come in with a little bit more, the electron is ripped of the metal, but it actually moves away then from the metal./nAnd so, in this case and in all cases, we have got to conserve energy. The incident energy of the light, from here to here, has to be equal to hv0 plus the kinetic energy, or if turn this around the kinetic energy is equal to the incident energy - hv0./nThis is an important expression. You need to know it. I won't give it to you on an exam. You don't have to memorize it, though. You just have to reason here conservation of energy. You can draw this diagram and figure it out./nNow, another very important point here that I am going to emphasize is that you absolutely, positively, no questions have to have a photon of at least this energy to get the electron off. What you cannot do is you cannot have, for example, a photon with half of this energy, Ωhv0./nOr, what you cannot do is have two photons come in with a half of this energy and make that electron come off. You have to have one photon to make this electron come off, and it has to have the frequency hv0. That's the particle-like nature of the radiation. Even though you have the same total amount of energy here, the fact that you cannot have two to pull the electron off, you have to have one and it has to have at least this quantum, at least that packet of energy./nThat's very important. All the problems you are going to do, if one photon comes in, you're going to get one electron off as long as that photon has hv0 of energy. Now what we've got to do is we have to do our own. Yes?/nIf the energy of the incident photon is twice the work function energy, yes, the electron will come off and the excess energy that doesn't go to the metal to pull the electron off goes to the kinetic energy of the electron./nAnd so if this incident energy is twice the work function, well, then the kinetic energy of that electron will be equal to the work function. I'm sorry? Two electrons won't come out. That's a good question. What she asked was if I put twice the amount of energy here with one photon, will I get two electrons out?/nNo, absolutely not. That is the quantum nature or the particle nature of the radiation. Let's do our own photoelectron experiment. Question?/nThose graphs up here, kinetic energy versus the frequency of light, those were the predictions from classical physics. Kinetic energy independent of frequency. Kinetic energy increasing with the intensity of light. Those are predictions from classical physics. How I got them, how I knew about them is something that we're not going to talk about because it's wrong./nIt's best at this point not to go through the logic of how I got that, but maybe after you have 8.02 it will become obvious to you. Good question. Let's do our own photoelectron experiment. Now we need the camera here. Let me get this started here./nWhat I also need are two volunteers to help us do this experiment. Come on down. Somebody else want to come? OK, come on down./nAll right. I have two volunteers here. Oh, I forgot to tell you that I need to do something so you've got to stay up here for a moment. I forgot to explain something. My fault. Sorry. Maybe you want to turn around. I forgot to tell you something here./nWhat we're going to do --/n-- is use this device here. This is an aluminum plate./nAnd you are going to see it here on the side walls. That is a picture of the device we've got up here. This is an aluminum plate. And that aluminum plate is mounted to a metal rod. That's that blue rod. And then there is a needle here in that blue rod and it's mounted on a pivot so it moves very easily. What we're going to do is we're going to put some excess charge on this metal plate./nAnd, when we do that, that needle is going to deflect. It's going to deflect because those excess charges, the electrons are going to run down that metal rod and then onto the needle. And since these electrons repel each other, and this is a very low friction pivot, this needle is going to move. And then what we're going to try to do is we're going to try to do the photoelectron experiment./nWe are going to come in and shine some UV radiation on this plate and see if we can eject electrons. That's what we're going to do. Now I've got my volunteers who are going to do this. Who wants to be the charger? Who wants to be the discharger? You'll be the charger, OK. This will be your weapon. You hold that. You hold that. Keep your fingers on the yellow plastic. This is going to be your weapon, the UV light./nI am going to need you in a moment so just stand by. What is your name? Don, OK. What you need to do is you need to take that Lucite rod and rub it really hard on the fur. And what that is going to do is the fur has some natural oil, and he is going to transfer a little bit of the natural oil onto that rod./nAnd there are some stray electrons around and some negative ions around, and they like to be on that oil. But then we're going to contact that rod with the aluminum plate and the electrons will go onto the aluminum plate. So, you've got to rub this really hard and then you've got to go and touch that and put the electrons on. And you should watch the needle move here. You've got to touch it on the edge, actually. Good./nWell, you charged it a little bit. That's not bad. Now take the rod again and rub it really, really hard. [LAUGHTER] Really hard. Touch the edge of the plate there. Touch the edge of the plate. [LAUGHTER]/nThis way. You've got it. Pretty charge there. Touch the edge of the plate. Fantastic. Now we need the discharger. You've got to come right here and shine the UV light on the base of it. You've got to get a little closer. Maybe turn your hand this way so that people can see it discharge. Fantastic./nTry it again. Come on, charge it up. [LAUGHTER] Really hard. Touch the edge of the plate. [LAUGHTER]/nThis way. This works the best. All right. Touch the edge of the plate. Let's get it. Fantastic./nMaybe just a little bit more. We can get more electrons. Hard, hard, hard, really hard. OK. Charge it up. Oh, OK. Discharge here. [LAUGHTER] Fantastic. What you saw was when the UV radiation then was incident on that aluminum plate the electrons were emitted and then the needle deflected back./nNow we've got to do this one more time. Why don't you come over here? What is your name? Jenny. Come on over here, if you can. And this time, after you charge it up, I am going to hold this glass Pyrex plate between the light and the aluminum plate./nAnd that is going to prevent the UV radiation from going through and so it shouldn't discharge. OK? All right. Go ahead. Let's charge it up one more time. You really do have to rub that oil on there. [LAUGHTER] Really hard. Touch it up here. Fantastic./nNow I am going to put the light there and now we are going to shine it. Oops, it's already discharging. You've got to do it one more time. You've got to do the control experiment here. Really hard. It's a little bit humid out today so it's a little bit harder to make this work. A little bit harder. Done. Get it up there./nAll right. Touch the side there. Good. That's pretty good. Fantastic. We've blocked the UV radiation. Electrons didn't jump off. Hey, this works. Thank you very much. Let's give them a hand. [APPLAUSE] Thank you very much. This photoelectron business, it's really real./nWhat I want to do now is I want to just work a couple of problems./nAnd here is the first problem. What it says is how many photons, at the radiation wavelength of one picometer, do you need to supply a pulse of energy that is a one joule pulse, say from a laser? It's a pulse laser. Suppose you want to supply one joule of energy in this light pulse./nThat is what the problem says, one joule in a pulse. Now, how do you work a problem? Lots of ways to work a problem. Sometimes I like to draw pictures. 1J, that's my one joule. I want 1J of energy. But I am told that I have radiation that has a wavelength of one picometer./nThat's 1 x 10-12 meters. That's the wavelength of my radiation. And I am asked how many photons do I need? Well, what do you know about a photon? We said that the energy of a photon is equal h0. That's one photon, the energy of a photon. The units here are joules./nImplied is joules per photon. And so I know the wavelength, I don't know the frequency here, but I know the relationship between wavelength and frequency. Frequency is equal to C over the wavelength. And so I can then calculate the energy, and when I do that it's 1.99 x 10-13 joules per photon./nCarrying one more digit than is significant because this is an intermediate step in our calculation. And now, if I want a plus of energy that is one joule and each photon has 10-13 joules per photon, well, that's 1.0J / 1.99 x 10-13 joules per photon./nWell, you can calculate that. It comes out to be 5 x 1012 photons. That's what I will need then. That's the answer then. Let me just write that down./nLet's work one more where we can understand./nThis is important because you need it for your homework. Here is the problem. You've got power of a radiation from a continuous laser. You turn on your laser, you've got power. What is power? Power is energy per unit time. We're going to use in our unit system the unit as power as watt./nA watt is a joule per second. It is how much energy is delivered per unit time. And we're told that we've got radiation of three milliwatts, that's 3.0 x 10-3 joules per second. The question is how long will it take for a total energy of one joule to be supplied?/nWell, 1.0J / 3.0 x 10-3 J/S = 330 S. And then, rushing through this, one more. How many photons at a radiation wavelength of one picometer again --/nHow many photons per second have to be delivered if the power of the radiation is three milliwatts? Power is 3.0 x 10-3 J/S. The radiation is one picometer, but we already calculated how many joules there are in radiation per photon with wavelengths of one picometer./nThat's 1.99 x 10-13 joules per photon. Joules cancel. And that means we're going to have to have 1.5 x 10-10 photons per second, because each photon has this much energy./nThis was the power. The rate at which we're delivering the energy, we're going to have the have this many photons per second coming out if the photons have that wavelength of one picometer. Great. See you later this afternoon or on Friday.
Tags //
Chemical Science Particle Nature Light
Added: April 16, 2009, 10:24 pm
Runtime: 2852.33 | Views: 16471 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science - Hydrogen Atom Wavefunctions - Lecture 7
Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 7/nTopics covered:
/nHydrogen Atom Wavefunctions/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 7/nAll right. Today, in particular the second half of the lecture today, we're going to do some of the hardest concepts that we've done so far, and also some of the most important concepts that we've done so far./nI just want to give you a heads-up on that. Last time we had we had solved the Schrödinger equation for the binding energies of the electron to the nucleus. And that means if I write the generic Schrödinger equation down here, what we found was what this E was./nAnd we found that it had a nice analytical form, that the allowed binding energies were quantized. They were quantized by that principle quantum number n. And so we can write those allowed energies as En=-Rh/n2./nSo, n is this principle quantum number. And n runs from 1, 2 all the way up to infinity. Today what we're going to do is we're going to look at the solutions to the Schrödinger equation for this, for the wave function, for the wave./nAnd remember we said that the wave, in some way, represents our electron. And today we are going to talk about exactly what is the meaning of the wave function. But, before we do that, I have to tell you that when you go to solve the Schrödinger equation for the wave function here what happens is that two more quantum numbers pop out./nAnd one of the quantum numbers that pop out in the solution for the wave function is a quantum number we call l. l is the angular momentum quantum number. It's called the angular momentum quantum number because it, in fact, determines how much angular momentum the electron has./nIt is a quantum number, which means it has allowed values, very specific values. The allowed values of l are the following. They are zero. Unlike n, the lowest value that l can have is zero. 0, 1, 2, 3 all the way up, but it has got a limit./nl has got a limit. The limit is n-1. So l can never be larger than n-1. It's tied to the principal quantum number. Why is it tied to the principal quantum number? Well, notice that only the principle quantum number tells you about the binding energy./nIt tells you about the total energy of this electron interacting with the nucleus. Whereas, the quantum number l, the angular momentum number, it determines how much angular momentum the electron has./nAnd, in a classical picture, you may be familiar with the fact that if something has got angular moment it has rotational kinetic energy. And since the total energy is that rotational kinetic energy plus potential energy, well, then l is never going to be as large as n because, otherwise, then the electron would only have rotational kinetic energy and no potential energy./nAnd that wouldn't work, right? So, that's why there is a limit here to l that is as large as n-1. Because you have to leave some energy to be potential energy here. And then, finally, we have the third quantum number./nAnd that third quantum number we call m. It is the magnetic quantum number. And it is called magnetic because, in fact, it does determine the behavior of an atom in a magnetic field. Although, we're actually not going to take a look at that./nBut more specifically what m is, is the z component of the angular momentum. And its allowed values are the following. n=0, so just like l it can have a value of zero, +1, +2 all the way up to +l. Look at this./nThe magnetic quantum number is tied to the angular momentum quantum number. Why? Well, because this is the z component of the angular momentum, or it dictates the z component of the angular momentum./nl dictated the total angular momentum. Well, the z component of the angular momentum is never going to be bigger than the total angular momentum, so that is why n is tied to l. And, of course, when we talk about a component, we're going to have a direction here, too./nAnd so these quantum numbers m can be zero plus/minus 1, plus/minus 2 all the way down to plus/minus l. So, that is it. We've got to have three quantum numbers here to really explain our system. The reason we have three quantum numbers is because we have a 3-dimensional system./nSo, it a little bit makes sense that you've got to have three quantum numbers to really describe the hydrogen atom here. And then the consequence of having these three quantum numbers, when you solve that differential equation, remember we talked last time where those quantum numbers come from when you solve a differential equation, as you will when you do 18.03./nThose quantum numbers come from imposing these boundary conditions on your differential equation. Those boundary conditions make a generic or general differential equation specific to the problem you're working on./nAnd when you do that, those quantum numbers fall right out. And, again, we believe them to be true because they agree with our observations of nature. Now we've got to deal with three quantum numbers that are going to have to then describe these states that we talked about last time./nFor example, we talked about the ground state, n=1 here. But what I'm saying to you now is that there are a few more quantum numbers that we have to add to label that ground state correctly. Or, to label it completely./nAnd, as I just said, if n=1, well, then we learned about l here. l, the largest value it can have, is n-1. So, we have a quantum number l that is tied here. And that quantum number is zero. l=0./nAnd we just learned that we have a third quantum number m. And the greatest value that m can have is +l. So, if l=0 then m=0. And so, therefore, our ground state, the label that we have got to put to our ground state is the 1, 0, 0 state./nSo, we're expanding our definition of the label of that state. Last time it was n=1. Now it is 1, 0, 0. And, if we have an electron in that 1, 0, 0 state, then we're going to have a wave function that describes that electron./nThat electron is going to be represented by a wave function. That wave function is psi 1, 0, 0. The energy of that 1, 0, 0 state is minus the Rydberg constant over 12. Just like we had last time. Now, suppose we had the first excited state, which was n=2, as we looked at last time./nIf n=2, what is the smallest value that l can have? Zero. And if l=0, what is the only value that m can have? Zero. We have now a state that is the 2, 0, 0 state. And, if you have an electron in the 2, 0, 0 state, we're going to describe that electron by a wave function that we're going to label psi 2, 0, 0./nAnd the energy of that state, we saw last time, minus the Rydberg constant over 4. But n=2, we also just saw that the quantum number l can have another value. And that is one. And if l=1, what is the largest value that m can have? One./nAnd so we've got another state here. It's the 2, 1, 1 state. And, if you've got an electron in the 2, 1, 1 state, that electron is going to be described by a wave function that we're going to call the psi 2, 1, 1 state, the psi 2, 1, 1 wave function./nNotice that the energy of this state is still minus the Rydberg constant over 4. It is the same as the 2, 0, 0 state. These two states are said to be degenerate. Degenerate means have the same energy./nIf n=2, then l=1. What's the next smaller value that m can have? Zero. So, we have a 2, 1, 0 state. If an electron is in that state, the wave function describing that electron is 2, 1, 0. Again, the energy here is minus the Rydberg constant over 4./nSame energy because the energy is only dictated by the n quantum number. And then, finally, what's the smallest value m can be if you have n=2, l=1? Negative one. So, we have a 2, 1, -1 state. The wave function describing that electron in that state is the psi 2, 1, -1 wave function./nNow, I described the electrons in these states by these wave functions ?. But there is another language, as I alluded to last time. Another language that is used to describe the wave functions. And that language is this orbital language./nWe talked last time how an orbital is nothing other than a wave function. It is the solution to the Schrödinger equation for the hydrogen atom. It is actually the spatial part of the wave function, meaning there is another part of the wave function called the spin part./nBut we will look at that a little bit later. And how are we going to label these wave functions in the orbital language? Well, we're going to label them by the principle quantum number n. And, of course, the angular momentum quantum number l and then a subscript here m for the magnetic quantum number./nBut what we do is instead of using the actual value of l, we have a letter code. For example, if l=0, we call that the s-orbital. In the case of the 1, 0, 0 state, if you have an electron in that state, the wave function that describes that electron is the 1s-orbital or the psi 1, 0, 0 wave function./nThis is the principal quantum number. This is the code s for l=0. And then, likewise, in the 2, 0, 0 state, the wave function that describes that electron will be 2s. Because here is the n=2 and then our code for l=0 is s./nNow, when l=1, again, we don't use l=1, we use a letter. That letter is p. We call that a p-orbital. This state here, the 2, 1, 1 state is going to be a 2p wave function, or the electron in it is going to be represented by this 2p wave function./nThe same thing for this state. They're all 2p because l=1 for all these three states and n=2. Now, if I had here an angular momentum quantum number of 2, we'd call that a d-orbital. If I had one that l=3, I would call that an f-orbital, and so on and so forth./nBut now, what I haven't said anything about yet, is the m quantum number here. Again, we've got a code for this. We're actually not going to use the number m. We are going to use some letters. And the code is that when m=0 we are going to put a z subscript here on this p-orbital designation, when m=0, when m=1 we're going to be an x subscript on this p-orbital designation and when m=-1 we're going to put a y subscript on this p-orbital designation./nNow, I should tell you that what I just did here is not actually correct. In other words, m=1 isn't really the x subscript and m=-1 isn't really the y subscript. The reason is because these two p wave functions, when m=1 and m=-1, they're complex functions./nAnd what we do is we do some linear combination of the m=1 and m=-1 wave functions to get what we call the px wave function and the py wave function. One is a plus linear combination. One is a negative linear combination./nYou're not responsible for that. Therefore, you are not responsible for knowing when m=1 we have an x and m=-1 we have a y. You are responsible for knowing when m=0, you have a x subscript here. Now, I should make one other point here./nAnd that is you see I don't have a subscript here for m on the s-orbitals. Well, in an s state, when l=0, there is only one possible value of m which is zero. And so we just leave out that subscript./nWe don't put a z here on the s designation. What does this mean, the fact that we've got these extra quantum numbers? Well, it means we have extra states. And these states, actually, though have the same energies that we saw last time./nBut let's try to expand that a little bit and draw an energy level diagram so that we really understand what is going on. Here is my energy level diagram, energy going up this way. And when n=1 then our quantum numbers, the most complete description here is the 1, 0, 0 state./nAnd the electron in that state has the wave function that is represents that electron. We call that the 1s wave function. That is the energy. When n=2 you see now we have now four different states that are all the same energy, 2s, 2py, 2pz, 2px./nThey have all the same energy. They are degenerate. Again, degenerate means having the same energy. And, in general, what we've got is n2 degenerate states at each end. So, these have all the same energy./nThey differ in how much angular momentum the electron has and how much angular momentum the electron has in the z direction if it were in the presence of a magnetic field. But they have the same energy because energy is only dictated by the n quantum number./nNow, when n=3, how many degenerate states do we have? Nine. Here they are. The energy is -1/9, the Rydberg constant. Here are the nine degenerate states. 3s, 3py, 3pz, 3px. That pattern just reproduces 2s, 2py, 2pz, 2px, so we won't go through those./nBut now we've got some extra states here. Again, their quantum numbers are all 3 for n, but when n=3 the largest value of l=2. And so all of these states here have l=2. And our code for l=2 where these d-state./nIf you have an electron in those states, it's represented by a 3d wave function. But now the reason these 3d wave functions differ is because they have different amounts of angular momentum in the x component./nThey have different values of m. If n=3, l=2. This smallest value that m can have is -2, right? And then I am going to just call, when m=-2, xy here in the subscript. When m=-1, I am going to put yz in this subscript./nWhen m=0, I am going to put z squared in this subscript. That is going to be my code for m=0. In the case of 3d orbitals, the 3d wave functions, I am going to put a z squared in that subscript. Then when m=1, I am putting an xz./nAnd when m=2 an x2 ñ y2. Again, you are now responsible for knowing when m=-2, this is xy, when m=-1, this is yz, because that isn't strictly correct. Again, we've complex functions. We're making them real./nAnd we're taking linear combinations. You are responsible for knowing that when m=0 in a 3d state, this subscript here is z2. When m=0 in a 2p state, that's a z subscript. When m=0 in a 3d state, that's a z2 subscript./nYou will look at these 3d states more in detail when we talk about transition metals in the second half of the course with Professor Drennan. So, that's our energy level diagram. Everybody OK with this? Questions? OK./nWe've found these two other quantum numbers. We've got three quantum numbers. We know how to label the states and we know how to label the wave functions that describe the electrons in these states, but now it's time to talk about what a wave function really means or how exactly does a wave function represent this particle, this electron? How do you interpret the wave function? And the answer is you don't./nThe answer is that that wave function is the wave function. It is one of these concepts that you cannot or you don't have a ready classical analogy. It's one of these concepts that you don't experience in your everyday life, and so you cannot say it's like this, because within your everyday world there is nothing to draw a correct analogy to./nHowever, the wave function squared does have a physical interpretation that is meaningful in your environment. And that is that this wave function squared, and let me just write it out here now in its full glory./nRemember, this wave function, we're going to denote by three quantum numbers, n, l and m, and it's a function of r, theta, phi. If I take this wave function and I square it, the interpretation of that wave function squared is that it is the probability density./nThat is it is a probability per unit volume. A density is always per unit volume. So, it's a probability per unit volume. Where did that come from? Good question. Soon after Schrödinger wrote down his wave equations, there was a lot of discussion in the scientific community about what does psi really mean? What is the interpretation of psi? And there were a lot of interpretations given, a lot of explanations given, but finally one very cleaver scientist by the name of Max Born said if I think of psi squared as a probability density then I can understand the predictions that the Schrödinger equation makes./nSo, psi squared is an interpretation. He said if I think of psi squared as the probability per unit volume and then I go an analyze all of the results of solving the Schrödinger equation in terms of that concept, that it is a probability density, then things make sense./nAnd those predictions agree with my observations. You know what? That's it. There is no derivation here of psi squared. Psi squared is just that. It is an assumption. It is an interpretation. But, you know what, you use that interpretation and that makes predictions that agree with our observations./nAnd there are no observations that even hint that that interpretation isn't correct. But that is it. You don't go any further. There's no derivation of this. This is an interpretation. It is a probability density./nWell, this gentleman, Max Born, was a really cleaver scientist. Max Born is the same Born of something called the Born-Oppenheimer approximation that maybe some of you know about. It is the same Borne of the distorted wave Born approximation, which probably nobody knows about./nBut I've got to tell you that despite the fact that Max Born has all of these accomplishments, the interpretation of size squared is a probability density, the Born-Oppenheimer approximation, the distorted wave Born approximation, despite all of those accomplishments, he is best known for being the grandfather of Olivia Newton-John./n[LAUGHTER] That is true. Actually, a couple of weeks ago in the Boston Globe, and I guess papers throughout the country, has a magazine called Parade Magazine. And it actually had an article about Olivia Newton-John, if somebody is going who's Olivia Newton-John, that's just an indication of how old I am./nOlivia Newton-John is a single. Grease. It was interesting. The Boston Globe a few weeks ago in Parade Magazine, there was an article on her. And it mentioned that her grandfather was Max Born. Didn't say anything about Max Born after that, but did mention that./nAll right. Now you know what size squared is. It's a probability density. You and I, we can understand that. Size squared, we can understand that. It's a probability density. But what I want to really emphasize here is that it is a probability density./nIt is not probability. It is probability per unit volume. That's important. In a moment, we're going to look at a quantity that is a probability. But this is a probability density. You've got to get the units correct here./nHow can we use that to understand something about where the electron is in an atom? Well, let's do that on the slide there. Kill those lights. Probability density. What I am going to do is I am going to represent the probability density here by a density dot diagram./nI am going to take my 1s-orbital, my 1s wave function, or my psi 1, 0, 0 wave function, and I am going to square it. And then I'm going to take the results of that squared function and plot it as a dot diagram here where the density of the dots is proportional to the probability density./nSo, the darker the dots the higher the probability density. And, as the dots get more and more dispersed, the probability density is getting smaller. I did that for my 1s wave function, squared the 1s wave function and plotted it here on x, y, z./nOh, I got the x and the y turned around. That's all right. I plotted it here. What you can see is that the probability density is a maximum at the origin, at the nucleus, and that it decays equally in all directions./nIt is isotropic. There is no angular dependence. It's spherically symmetric. And that you can also see nicely if you look at the actual plot of the wave function. Not size squared now. The wave function, which I am plotting here./nThis is the wave function and I am plotting it versus r. Actually, what I am plotting it here is as r over this something called the ìa knotî. aO is a constant. aO is called the Bohr radius. aO is about a half an angstrom./nI will explain to you where aO comes from in a little bit, but right now it's just a constant. Here is the actual form of that wave function. It's pretty simple. This stuff right in here, this is all a constant./nJust one over pi aO cubed. I said this was about a half an angstrom. And then the important part is right here. It's a decaying exponential in r, e to the minus r over a knot. And so the wave function starts out at some high finite value at r=0 and it drops off exponentially as r goes to infinity./nThat's what we're plotting. And you can see that reflected here. When you square this you can see that reflected in that probability density. What does it tell me? It tells me that the probability density is highest at the nucleus and drops off in an exponential fashion equally in all directions./nThis is spherically symmetric. We're going to say some more about where is the electron in a moment after we go through not only 1s, but 2s and 3s. Here I plotted the 2s wave function. I took the 2s wave function, I squared it, so I got values as a function of r./nAnd, again, the density of the dots is proportional to that wave function squared. And, again, what do you see? You see that the probability density is largest at the origin. And that it decays again equally in all directions because it's spherically symmetric./nAnd it decays so much that all of a sudden you get to some value of r and there is no probability density. And then, as you get to the large value of r, well, the probability density increases again right here./nAnd then it finally decays as you get to larger values of r. What this wave function has in it here is something called a node. There is a value of r right in here where there is no probability density./nThat value of r, in terms of this constant, aO, is two times aO. We call that a radial node. You can see that radial node very easily if you look at a plot of the actual wave function. We're not squaring the wave./nThis is the wave function. Here it is. Here is the form for it. At r is equal to zero, it's some finite large value, and it decreases. It decreases until we get to a value of zero, psi=0. Let me just draw that here on the board./nI am plotting here the psi 2, 0, 0 wave function, the 2s wave function. I am plotting it as a function of r. What it looks like is that at r=0, it starts out as some high finite value and it drops./nAnd it actually goes through a zero. And it drops and it keeps dropping until some point and becomes negative. And then it turns around and it approaches a zero again. And so at very large r the wave function is zero./nRight here, where this wave function becomes zero, that's what we call a radial node, r=2aO. This is a radial node. It is a value of r that makes the wave function be equal to zero. If you wanted to solve for the radial node, you'd simply take the functional form for 2s, which is º(ΩpaO3)Ω (2-r/aO) e-r/2aO./nIf you wanted to solve for the value of r at which this node occurs, you set everything equal to zero. You solve for r. This goes away. This stuff is just a constant. It goes away. You have 2-r/aO and that's equal to zero./nYou can see, when you solve this, that r is equal to 2aO. That is the value of r at which you have a node. Now, notice this. At r=aO the wave function changes sign. It was positive up here. It is negative down here./nThat is a general characteristic. When the wave function goes through a node, the wave function changes sign. Why is that important? Well, have you maybe in high school -- We haven't talked about p orbitals yet./nBut remember you put sometimes a plus sign on a p orbital and a minus sign on a p orbital? Did you do that? Yeah? Well, that plus and the minus represented the sign of the amplitude of the wave function./nPlus meant it had a positive amplitude. Minus meant it had a negative amplitude. That's what it meant. Sometimes you may have called it the phase of the wave function. You know why that's important, the phase of the wave function? It's important because when you go to do chemical bonding, when you bring up two atoms and you are overlapping two atoms and you're overlapping the wave functions that have the same sign, you've got constructive interference and you have chemical bonding./nIf you come in and you overlap two wave functions that have opposite signs, you've got destructive interference and you've got no chemical bonding. We're going to see that later, but that's why that's so important, is the amplitude of the wave function here and these nodes./nLet's look at the 3s wave function. Here we are back up here. Plotted the 3s wave function. The probability density of the 3s wave function. Again, what do you see? You see right in the center, probability density is the largest./nAnd then, as r increases, that probability density drops off. However, you get to a value of r right here where you've got another node, another value of r that makes the wave function be equal to zero./nAnd then, as you increase r, the wave function again, the probability density increases. It increases because look right here. You're getting a more and more negative value. If you square a negative value you're going to get a large positive value./nThat is what this high probability density reflects. It reflects the fact that the wave function right in this area has a large negative value. You square it. You're going to get a large positive value./nAnd then, as you increase r again, well, again you get another value of r where you have a node. The wave function goes to zero. Here's that point right there. Here is psi=0. Wave function zero. And then, as you increase r, well, again, the probability density goes up./nWhy? Because the wave function increased right here. See that? Square it. It's going to go up. And then it turns around and goes to zero and this decays. If you wanted to solve for this radial node and this radial node, which I will let you do, you take the functional form, set it equal to zero and solve for r./nThat is easy. All of this stuff is a constant. This goes away. It's the quadratic and you're solving for the roots. So what have we learned? We've learned the 1s wave function, 2s wave function, 3s wave function./nAnd, in fact, all s wave functions or l=0 wave function, all of them are spherically symmetric. They have no angular dependence. Remember we said that in general the wave function depends on r, theta and phi./nS wave functions have no theta and phi dependence in them, unlike p wave function, which we will look at very soon. Also, very important here, the probability density of all s wave functions is a finite value at r=0./nThose are the two important things. And you know how to solve now for a radial node. You set the wave function equal to zero, solve for the value of r that makes the wave function zero. Now, we have to continue this discussion so we can start to talk about the probability of finding an electron some distance from the nucleus./nWe just talked about probability density. We haven't talked about probability yet. And here comes probability. We're going to plot something and we're going to talk about something called the radial probability distribution./nWhat is that? Well, the radial probability distribution is the probability of finding an electron in a shell. You know what a shell is. A shell is a sphere, but the sphere is hollow except that at the diameter or at the circumference you have a thin coating./nThat thinness has got a dr to it. It has a thickness to it. I'm sorry. It's a probability. This radial probability distribution is the probability of finding an electron in a shell of radius r and a thickness dr./nLet me try to explain that some more. Here is this gray part. That's my probability density that I drew before, the dot diagram. This is a 1s wave function. This is a probability density for the 1s wave function, ? 1, 0, 0 squared./nThis blue thing here is a spherical shell. It has some radius here r. It also has some thickness dr. You see I cut away here, this thickness dr? The radial probability distribution is the probability of finding this electron in this spherical shell that is of radius r and thickness dr./nSo, it's the probability of finding the electron at some distance r to r plus dr. That's the radial probability distribution. Now, I want you to notice what is the volume here of this spherical shell? Well, that volume is just 4pi r square, the surface area of that spherical shell, times the thickness which we're going to call dr./nThat is the volume. Now, if I wanted a probability of finding my electron in an s wave function some distance from the nucleus, some distance r to r+dr, what am I going to do? Well, I'm going to take my probability density, which I said was psi squared probability per unit volume./nI am going to multiply it by a volume. Then I am going to get a probability of finding my electron some distance r to r+dr from the nucleus. And that is what we're going to talk about on Monday, is the actual probability of finding the electron from the nucleus./nSee you on Monday.
Tags //
Hydrogen Atom Wavefunctions
Added: April 16, 2009, 10:28 pm
Runtime: 2999.40 | Views: 17633 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science - Hydrogen Atom - Lecture 6
Chemical Science/n * Email this page/nVideo Lectures - Lecture 6/nTopics covered:
/nThe Hydrogen Atom/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 6/nAll right. Let's get going. Where were we? We were at the point where we started out the course wondering about the structure of the atom, how the electron and the nucleus hung together. And we saw that we could not explain how that nucleus and electron hung together using classical ideas, classical physics, classical mechanics and classical electromagnetism./nAnd so we put that discussion aside and started to talk about the wave-particle duality of light and matter. And we saw that both light and matter can behave as a wave or it can behave as a particle./nAnd we needed that discussion in order to come back to talk about the structure of the atom. And, in particular, what was so important last time that we met is that we saw the results of an experiment, that Davidson, Germer and George Thompson experiment that demonstrated that mass of particle could exhibit wave-like behavior./nWe saw the interference pattern of electrons reflected from a nickel single crystal. An actual original paper that reports that result is on our website. You're welcome to take a look at it. But that really was the impetus, this observation of the wave-like behavior of matter./nThat was the impetus for this gentleman here, Erwin Schrödinger in 1926-27 to write down an equation of motion for waves. That is he thought maybe the answer here is that if particles can behave like waves then maybe we have to treat the wave-like nature of particles, the wave-like nature of electrons, in particular in the case when the wavelength, the de Broglie wavelength of the particle or the electron is comparable to the size of its environment./nMaybe in those cases we have to use a different kind of equation of motion, a wave equation of motion. And that is what he did. So, he wrote down this equation. We briefly looked at it last time. This equation has some kind of operator called the Hamiltonian operator./nIt has a hat on it, a carrot on the top of it. That tells us it is an operator that operates on this thing, psi. That psi is what's going to represent our particle. That psi is a wave, since we're going to give it a functional form in another day or so we're going to call it a wave function./nSomehow that psi represents our particle. Exactly how it represents our particle is something we're going to talk about again in a few days. But right now the important thing is to realize that this psi represents the presence of a particle, in this case the electron./nAnd when H operates on psi we get back psi. We do this operation and out comes psi again, the original wave function, but it's multiplied by something. That something is the energy. It's the binding energy./nIt's the energy with which the electron is bound to the nucleus. This equation is an equation of motions. This wave equation, Schrödinger's equation is to this new kind of mechanics, called quantum mechanics, like Newton's equation of motion, and I show you just the second law here, are to classical mechanics./nThis equation here tells us how psi changes with position and also with time. It tells us something about where the electron is and also tells us where the electron is as a function of time. It's an equation of motion./nAnd this is what Schrödinger realized, is that maybe when the wavelength of a particle is on the order of the size of its environment you have to treat it with a different equation of motion. You can no longer use F = ma, this classical equation of motion./nYou have to use a different equation of motion. And that's Schrödinger's equation, this wave equation. Can we dim the front lights a little bit? Because the screen is just a little bit hard to see, I think./nWe are going to let your electron be represented by this wave ?. And so psi, since it's going to be representing the electron, is going to be a function of some position coordinates, and also in the broadest sense a function of time./nNow, we, of course, can label psi in Cartesian coordinates giving it an x, y and z. If I gave you x, y and z for this electron in this kind of coordinate system where the nucleus is at the origin of the coordinate system, if I give you x, y and z coordinates, you'd know where the electron was./nBut it turns out that this problem of the hydrogen atom is really impossible to solve if I use a Cartesian coordinate system. So, I am going to use a spherical coordinate system. How many of you are familiar and have used a spherical coordinate system before? A few of you./nNot all of you. Well, it's not hard to understand. And it is important that you understand it. So, instead of giving you an x, y and z to locate this electron, this particle in space, we're going to give you an r, a T and a ?./nAnd the definitions of r, T and ? are the following. If here is my nucleus at the origin and here is the electron, r is the distance of that electron from the nucleus. It's just the length of this line right here./nThat's one coordinate. A second coordinate is T. T is the angle that this r makes from the z axis. And then the third coordinate is psi. Psi is the following. If I take that electron and I just drop it perpendicular to the xy plane, and I then draw a line in the xy plane from that point of intersection to the origin, the angle that that line makes with the x-axis here is ?./nSo, I am going to give you an r, a T and a ?. R is just the distance of the electron from the nucleus. T and psi tell us something about the angular position. And then, as I said, in the largest sense, there is also time./nBut we'll talk about time a little bit later. Psi represents our electron. Now, what does the Schrödinger equation specifically, for a hydrogen atom, actually look like? This Hpsi times Epsi is kind of generic Schrödinger equation./nAnd now we've got to write a specific one, one specific for the hydrogen atom. We need to know what this is, H. That's our Hamiltonian, our operator. And so the operator here for that hydrogen atom is this./nWhat is it is essentially three second derivatives, one here is with respect to r, a second is a second derivative effectively with respect to T, and another one, the final one is a second derivative with respect to psi./nIn other words, if this whole Hamiltonian is operating on psi, what you're going to do is essentially take the first derivative of psi with respect to r, multiply it by r2. And then take a first derivative with respect to r again and multiple it by 1 / r2./nAnd add to that the first derivative of psi with respect to T multiplied by psi and T, etc. You don't have to know this. I'm just showing this to you so you recognize it later on. This is a differential equation./nIn 18.03, you learned how to solve these differential equations. And then there is another very important term here, so it's all of this plus this, u of r. What is u(r)? Potential energy of interaction./nAnd the potential energy of interaction, of course, is the Coulomb potential energy right here, one over r dependence. We've talked about the Coulomb force. This is the potential energy of interaction that corresponds to the Coulomb force./nSo, that's the specific Schrödinger equation for the hydrogen atom. Now, what we have got to do is we have to solve this equation for the hydrogen atom. And when I say solve this equation, what I mean is we're going to have to find E, these binding energies of the electron to the nucleus./nThat is part of our goal when we say solve this differential equation is knowing what E is, is figuring out what E is. And, actually, this is what we're going to do today, finding those energies. But then the second goal is to find psi./nWe want to find what is the functional form of psi that represents the electron and the hydrogen atom? Therefore, we're going to want to find the wave functions for psi. And, you know what, those wave functions are nothing other than what you already sort of know, and that is orbitals./nYou talked in high school about S orbitals and P orbitals and B orbitals. Those orbitals are nothing other than wave functions. They come from solving Schrödinger's equation for the hydrogen atom./nThat's where they come from. Now, specifically the orbital is something called the spatial part of the wave function as opposed to the spin part. But for all intents and purposes they are the same./nWe're actually going to use these terms interchangeably, orbital-wave function, wave function-orbital. The bottom line is that when you solve Schrödinger's equation for the energy and the wave function it makes predictions for the energies and the wave functions that agree with our observations, as we're going to see today, in particular for the case of the binding energies of the electron to the nucleus./nThis equation predicts having a stable hydrogen atom, a hydrogen atom that seemingly lives forever in contrast to when we use classical equations of motion. When we used classical equations of motion we got a hydrogen atom that lived for all of 10-seconds./nBut here we finally have some way to understand the stability of the hydrogen atom. It makes the Schrödinger equation, it makes predictions that agree with our observations of the world we live in./nAnd, therefore, we believe it to be correct. That is it. It agrees with the observations that we make. Let's start. And we're actually not going to solve the equation, as I said, but you will do so if you take 5.61, which is the quantum course in chemistry, or 8.04, I think it is, which is the quantum course in physics after you take differential equations so that you know how to solve the differential equations./nBut we're going to write down the solution in particular here for E, the binding energies of the electrons to the nucleus. Now we're going to need this. We've got H? = E?. And when we solve that equation, we get the following expression for E, these binding energies./nE = 1 / n2 (me4/8?o2 h2). That is what we get out of it. And there is a minus sign out in front. Now, what is m? M is the mass of the electron. What is e? E is the charge on the electron. Eo is this permittivity of vacuum that we talked about before./nIt's really just a unit conversation factor here. H is Planck's constant. Here comes Planck's constant again. It is ubiquitous. It's everywhere. And what we do is that we typically take all of these constants and group them together into another constant that we call the Rydberg constant./nAnd we denote it as a RH. All of that is equal to RH, so this is over n2, minus 1. And the value of RH, that Rydberg constant, and this is something you're going to need to use a lot in the next few weeks, is 2.17987 times 10 to the negative 8 joules./nBut you also see, in this expression for the binding energies of the electron to the nucleus, that there is this n here. What's n? N is an integer. When you solve that differential equation, you find that n has only certain allowed values./nN can be as low as 1, 2, 3, and n can go all the way up to infinity. N is what we call the principal quantum number. I am going to explain that a little bit more by looking right now at an energy level diagram./nThat is the expression. But now let's plot it out so that we can understand what is going on here a little more. We are going to be plotting this expression as n goes from 1 to infinity. I have the energy access here./nEnergy is going to be going up in that direction. When n is equal to 1, the binding energy of that electron to the nucleus is effectively the Rydberg constant. Here I rounded it off, minus 2.18 times 10 to the negative 18 joules./nBut our expression here says that there can be another binding energy of the electron to the nucleus. It says that n can be equal to 2. And if n is equal to 2, well, then the binding energy of the electron is one-quarter of the Rydberg constant, because it is the Rydberg constant over 22./nIf n is equal to 3, well, our expression says that the binding energy is minus one-ninth of the Rydberg constant. If n is equal to 4 it is minus a sixteenth of the Rydberg constant, n is equal to 5, minus a twenty-fifth, n equal to 6, minus a thirty-sixth, n equal to 7, minus a forty-ninth, all the way up to n equals infinity./nAnd you know what the value of the binding energy is when n is equal to infinity? Zero. Our equation says that the electron can be bound to the nucleus with this much energy or this much energy or this much energy and so on, but it cannot be bound to the nucleus with this much energy, somewhere in between, or this much energy or that much energy./nIt has to be exactly this, exactly this, exactly this, so on and so forth. That is important. What we see here is that the binding energies of the electron to the nucleus are quantized, that that binding energy can only have specific allowed values./nIt doesn't have a continuum of values for the binding energy. Yes? Those are identically the same size. Because this is an operator, right? I left the hat off here. Remember that we took a second derivative of psi? So, you cannot cancel this./nThis is an operator taking the derivative of psi. You cannot just cancel that. This is to multiply by on this side. This side is. This is E times psi, but not over here. That's really important./nWe have these quantization of the allowed binding energies of the electron to the nucleus. Where did that quantization come from? That quantization came from solving the Schrödinger equation. It drops right out of solving the Schrödinger equation./nHow did that happen? Well, in differential equations, as you will see, when you solve a differential equation, what you have to do to solve it so that it adequately describes your physical situation is you have to often impose boundary conditions onto the problem./nAnd it's that imposition of boundary conditions that gives you that quantization. That is where it comes from mathematically. In other words, remember one of those angles that I showed you, the phi angle? You can see it would run from zero to 360 degrees./nBut you also know, if you go 90 degrees beyond 360 degrees, suppose you to go to 450 degrees, well, that should give you the same result as if you had F = 90. What you have to do is you have to cut off your solution at 360 degrees./nWhen you cut off that solution, well, then that gives you, in these differential equations, these quantization. That is physically where it comes from. Again, this is not something you're responsible for, but when you do differential equations later on in 18.03, you will see how that happens./nLet's talk some more about these loud energy levels. When the electron, or when n = 1, the language we use is that we say that the hydrogen atom, or we say that the electron or the hydrogen atom is in the ground state./nWe call this the ground state because this is the lowest energy state. It has got the most negative energy. It's the lowest energy state. We call n = 1 the ground state of the hydrogen atom or the ground state for the electron./nWe use those terms of the electron or the hydrogen atom interchangeably. Now, what's the significance of this binding energy? And this is important. The significance is that the binding energy is minus the ionization energy for the hydrogen atom, because if I put this energy in from here to there into the system then I will be ripping off the electron and will have a free electron./nSo, the ionization energy is minus the value of this binding energy. The ionization energy is always positive. The binding energy, the way we're going to treat this, is going to be negative because the electron is bound./nAnd then the separated limit, the electron far away from the nucleus, well, that energy is zero. So, the binding energy is minus the ionization energy or conversely the ionization is minus the binding energy./nThat is the physical significance of these binding energies. And when we talk about an ionization energy for an atom, we are typically talking about the ionization energy when the atom is in the ground state./nThis is the ionization energy we're talking about. But we also said that the binding energy of the electron can be this much meaning it's in the n = 2 state. That can be possible also. Not at the same time as it's in the n = 1 state, but you can have a hydrogen atom in a state, which is the n = 2 state./nWhat that means is that the electron is bound by less energy. When that is the case, we talk about the hydrogen atom being in the first excited state. This is the ground, this is the first excited state, but n is equal to 2./nIn that case, the electron is not as strongly bound because it is going to require less energy to rip that electron off. The binding energy is n = 2 is minus the ionization energy if you have a hydrogen atom in the first excited state./nMake sense to you? Yeah. OK, so we can have atoms in this state, too. Then the ionization energy is less. It takes less energy to pull the electron off. Yes? In everything that we are going to deal with, we are going to have binding energies that are negative./nLet's do that. You can, of course, have a binding energy that is positive, but the problem is that isn't a stable situation. OK. Good. Other questions? Yes. When we're dealing with a solid, we talk about a work function as opposed to an ionization energy./nWhen we're dealing with an atom or a molecule, we talk about an ionization energy as opposed to the work function. It's really the same thing. Historically there is a reason for calling the ionization energy off of a solid the work function./nOh, one other thing. I just wanted to point out again right here is that when n is equal to infinity the binding energy is zero. That is the ionization limit. That is when the electron is no longer bound to the nucleus./nNow, one other point here is that this solution to the Schrödinger equation for the hydrogen atom works. It predicts the allowed energy levels for any one electron atom. What do I mean by one electron atom? Well, helium plus is one electron atom./nBecause helium usually has two electrons, but if you take one away you have only one electron left. And so this helium plus ion, that's a one electron atom, or if you want to say it more preciously one electron ion./nOr, lithium double plus, that's a one electron atom or a one electron ion. Because lithium usually has three electrons, but if you take two away and you only have one left that's a one electron atom./nUranium plus 91 is a one electron atom. Because you took 92 of them away, one is left, that's a one electron atom or an ion. And the bottom line is that this expression for the energy levels predicts all of the binding energies for one electron atoms as long as you remember to put in the Z2 up here./nFor a hydrogen atom that is, of course, Z = 1, so we just have -RH / n2. But for these other one electron atoms you have to have the Z in there, the charge on the nucleus. Why? Well, because that Z comes from the potential energy of interaction./nThe Coulomb potential energy of interaction is the charge on the electron times Z times E, the charge on the nucleus. That is where the Z comes from. That is important. How do we know that the Schrödinger equation is making predictions that agree with our observations? Well, we've got to do an experiment./nAnd the experiment we're going to do is we're going to take a glass tube like this. We're going to pump it out and we're going to fill it with hydrogen, H2. And then in this glass tube there are two electrodes, a positive electrode and a negative electrode./nAnd what I am going to do here is I am going to crank up the potential difference between these positive and negative electrodes, higher, higher, higher until at a point we're going to have the gas break down, a discharge is going to be ignited, just like I am going to do over here./nDid I ignite a discharge? Yes. There it is. And the gas is going to glow. We are going to have a plasma formed here. Oh, and what happens in this plasma is that the H2 is broken down into hydrogen atoms./nAnd these hydrogen atoms are going to emit radiation. That is some of the radiation that you're seeing here in this particular discharge lamp. We are going to take that radiation and we're going to disburse it./nThat is we're going to send the light to a diffraction grading. This is kind of like the two-slit experiment. And when you look at it you're going to see constructive and destructive interference./nBut when you look at the bright spots of constructive interference you're going to find that those bright spots now are broken down into different colors, purple, blue, green, etc. And that is because the different colors of light have different wavelengths./nAnd if they have different wavelengths, well, then the points in space of maximum constructive interference are going to be a little different. And so we're going to literally separate the light out in space depending on their colors./nAnd we're going to see what colors come out of this. And so now, in order to help you do that, we've got some diffraction grading glasses for you. You should put them on and look into this light. And you will be able to see off to your left and to the right some very distinct lines./nAnd if you look into the lights above you can see all different colors from the white light. All right. Do you see the hydrogen lamp? I know that the white lights above the room are more interesting because there is a whole rainbow there./nI am going to turn the lamp a little bit since not all of you, if you are way on the side, can see it. I am going to start over here and I am going to turn the lamp a bit. Can you see that now? You should see a bunch of lines here to your left and some to your right./nAnd then, of course, you will see some up here. But they will probably dispersed best to your left and to your right. Pardon? Can we dim the bay lights? Can we dim those big lights over there? Probably not./nI am going to turn it over here. Can you see it? The spectrum that you should see is what I am showing on the center board there. You see it? Pardon? You have to look at the light. Oh, thank you./nThank you very much. Can you see that better? I will turn it back there. Do you see the emission spectrum now? It's a little better. Let's see if we can try to understand this emission spectrum that you're seeing./nWhat you should see the brightest is a purple line. No? Well, let's see. The purple line is actually rather weak, I have to say. If you come really close you can see it. And you're invited to come up a little bit closer./nThe purple line is kind of weak. What did I do? [LAUGHTER] Oh, I see. Yes. Interference phenomena work. Hey, look at that. [LAUGHTER] Fantastic. All right. The purple line is kind of weak, but the blue line is really strong./nAnd then there is a green line, which is also a little bit weak. And I can see because I'm really close, well, I'm not going to tell you that. There is a green line there. And then there is this red line./nLet's see if we can understand where these lines are coming from. What is happening is that this discharge, not only does it pull the H2 apart, break bonds, make hydrogen atoms, but it puts some of those hydrogen atoms into these excited states./nAnd so a hydrogen atom might be in this excited state. This initial excited state, high energy state. And, of course, that's a high energy state. It is unstable. The system wants to relax. It wants to relax to a lower energy state./nAnd when it does so, because it's going to lower energy state, it has to emit radiation. And that radiation is going to come out as a photon whose energy is exactly the energy difference between these two states./nThat's the quantum nature here of the hydrogen atom. The photon that comes out has to have an energy psi e which is exactly the energy of the initial state minus that of the final state. And, therefore, the frequency of that radiation is going to have one value given by this energy difference divided by Planck's constant H./nThat is what's happening in the discharge. What we've got is some hydrogen atoms excited to say, for example, this B state, which is a lower energy state, and so when it relaxes there is a small energy difference between here and this bottom state./nTherefore, you are going to have a low frequency of radiation. If you have some other hydrogen atoms in the discharge that are excited to this state up here, well, this is a big energy difference. And so psi e is going to be large./nAnd, therefore, you're going to have some radiation emitted that's at a high frequency because psi e is large. If it's at a high frequency, it's going to have a short wavelength. These hydrogen atoms are going to have a low frequency emission./nIt's going to be a long wavelength. So, we've got a mixture of atoms in this state or in this state or in any other state in this discharge. Now, let's try to understand this spectrum. And to do that I have drawn an energy level diagram for the hydrogen atom./nHere is n = 1 state, n = 2, n = 3, n = 4, all the way up to n = 0 here on the top. They get closer and closer together as we go up. This purple line, it turns out, or the purple color comes from a transition made from a hydrogen atom in the n = 6 state to the n = 2 state./nThe final n here is 2. The blue line comes from a hydrogen atom that has made a transition from n = 5 also to n = 2. The green line is from a hydrogen atom that makes a transition from n = 4 to n =2 and then the red line from n = 3 to n =2./nOf course, the transition from n = 3 to n = 2 is the smallest energy. Therefore, it is going to be the longest wavelength. n = 6 to n = 2 largest energy. Therefore, it is going to have the smallest wavelength./nNow, how do we know that these frequencies agree with what Schrödinger predicted they should be? Well, to know that, what we're going to do is we're going to write down this equation here, which is just telling us what the frequency of the radiation should be psi e over H./nBut we're going to use the predictions from the Schrödinger equation and plug them into here to calculate what the frequency should be. We were told here that the energy, say, of the initial state given by the Schrödinger equation is -RH / the initial quantum number squared./nWe're going to plug that into there. The final state, well, that's also the expression for the energy, we're going to plug that into there. We're then going to rearrange that equation so we get the frequency is the Rydberg constant over H times this quantity 1 / nf2 - 1 / ni2./nAnd since I told you here that all of these lines -- The final quantum number is 2. We can plug that in. And then we can just go in and put in 3, 4, 5, 6 and get predictions for what nu is for the frequency./nAnd what you would find is that predictions that this makes, the Schrödinger equation makes agrees with the observations of the frequencies of these lines to one part and 108. There is really just remarkable agreement between the energies or the frequencies predicted by Schrödinger equation and what we actual observe for the hydrogen atom./nHere is another diagram of the energies of the hydrogen atom n = 1, n = 2, n = 3. And the four lines that we were looking at where shown right here. These are the four lines. Here is n = 6 to n = 2, n = 5 to n = 2./nThese lines are actually called the Balmer series. I want you to know that there is also a transition from n = 6 to n = 1. It is over here. But you can see that that transition is a very high energy transition./nThat transition occurs in the ultraviolet range of the electromagnetic spectrum. And, therefore, you cannot see it, but it is there. Actually, what you can see is that there are transitions from these higher energy states to the ground state, transitions from all of them to the ground state, but they're all in the ultraviolet range of the electromagnetic spectrum./nThat is why you cannot see that right now. But those lines are called the Lyman series. And then there are transitions here to the n = 3 state. These transitions from the larger quantum number to n = 3 are called the Paschen series./nThey occur in the near infrared. Brackett series in the infrared. Pfund series in the far infrared. I got that backwards. And these different series are all labeled by the final state. And they're labeled by the names of the discoverers./nAnd the reason there are so many different discoverers is because in order to see the different kinds of radiation, you have to have a different kind of detector. And, depending on what kind of a detector an experimentalist had, well, that will dictate then what he actually can see, what kind of radiation, which one of these transitions he can view./nNow, we looked at emission. But it is also possible for there to be absorption between these allowed states of a hydrogen atom. That is we can have a hydrogen atom here in a low energy state, the initial state Ei./nAnd if there is a photon around whose energy matches the energy difference between these two states, well, then at photon can be absorbed by the hydrogen atom. Again, the energy of that photon has to be exactly the difference in energy between those two states./nIt cannot be a little larger. If it is a little larger that photon is not going to be absorbed. That's important. That's the quantum nature again of the hydrogen atom. They are specific energies that are allowed and nothing in between./nAnd then from knowing the energy of the photon you can get that frequency. And then in the case of absorption, the frequencies of the radiation that can be absorbed by a hydrogen atom are given by this expression./nThis expression differs from the frequencies for emission only in that I've reversed these two terms. This is 1 / ni2. This is 1 / nf2. I have reversed them so that you come out with a frequency that is a positive number./nFrequencies do have to be positive. So, we've got two different expressions here for the frequency depending on whether we're absorbing a photon or we're emitting a photon. Questions? I cannot see anybody./nThere. Epsilon knot is a conversion factor for electrostatic units. That is all you need at the moment. In 8.02 maybe you will go through the unit conversation there to get you to SI units.
Tags //
Chemical Science Hydrogen Atom
Added: April 16, 2009, 10:31 pm
Runtime: 2844.33 | Views: 23553 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science - Periodic Trends in Elemental Properties
Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 10/nTopics covered:
/nPeriodic Trends in Elemental Properties/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 10/nLast time we were talking about the energies of the various states in the multi-electron atom. Now, the question is experimentally how do we know what these energies are? How do we know these energy levels exist?/nAnd the primary technique that we have to know that is something called x-ray photoelectron spectroscopy. And x-ray photoelectron spectroscopy uses the same principle that we talked about when we talked about photo emission or the photo electric effect really explained by Einstein. And, by the way, I put on the website a very comprehensible article on Einstein's contribution to the photoelectric effect./nThis is something that just came out in a journal just very recently and I saw it. And so I urge you to take a look at it because it really is very understandable and kind of fills in some of the gaps that I left in talking about the actual problems, some of the kind of sociological effects or gaps./nAll right. So same idea, photoelectron spectroscopy and that we come in with a photon and that induced an electron to be emitted. But unlike the photoelectron spectroscopy on a solid where we essentially had just one energy level, in photoelectron spectroscopy on atoms we're going to have many energy levels as we've already seen./nAnd the photon that we're going to use, that photon is going to have an energy so that in principle it can pull out of the atom the most strongly bound electron. And if we want that, well, then that means that we're going to have to use a pretty energetic photon and that is we're going to use an x-ray photon./nSo it works in the following way. Let's take this unsuspecting neon atom. We bring in a photon, an x-ray photon. [LAUGHTER] I'll turn it down a little bit. Not too much. And that, of course, one of those electrons can be emitted. And one of the electrons that can come off is this p electron here so that the resulting ion configuration of the neon atom is 1s2 2s2 2p5./nBut also this photon can pluck off this s electron so that the resulting ion configuration is 1s2 2s1 2p6. And, of course, that photon can come in and pluck off an s electron so that the resulting ion configuration here is 1s2 2s2 2p6./nSo that one photon, in principle, has enough energy to pull off even the most strongly bond electron. And then what we do in this technique is that we measure the kinetic energies of these electrons that are emitted, and then we plot the number of electrons emitted at a particular energy. We scan the kinetic energy. And a typical plot looks like this./nThis is just the number of electrons coming off with the particular energy. And you see we see three different kinetic energies. We see electrons coming off with 383 eVs, electrons coming off with 1205 and electrons coming off with 1232 eV. Well, of course it's going to turn out here that those electrons that come off with the lowest kinetic energy are those electrons that were most strongly bound./nThere are those electrons that were in that 1s state. Why? Well, look at the energy level diagram here. Here are those 1s electrons. Here is the incident energy of the photon that we came in with. If these electrons are most strongly bond then they're going to have the highest ionization energy, the highest energy to pluck them off./nAnd, therefore, in order to conserve energy, the incident energy, the ionization energy plus that kinetic energy has to equal that incident energy. And if this is the largest energy, well, then those are the electrons that are going to have the lowest kinetic energy. So those are those 1s electrons. That's how we identify those. And then there are electrons coming off at 1205 where those are the electrons from the 2s state./nThat's a little bit higher energy. And so if this is the energy of the incident photon, it's a photon coming in as the same energy. If that's the energy of the incident photon this is then the ionization energy for those electrons in that 2s state. Well, that leftover energy then, that's the kinetic energy. And it is a little bit greater than it was for 1s because, again, those electrons are less strongly bound./nAnd then finally we have this feature here, 1232 eV. Those are the 2p electrons. These electrons are least strongly bound. So here is the incident energy of the photon. Here is the ionization energy of those electrons in the 2p state. The resulting or the leftover energy here is the energy that goes into the kinetic energy of those electrons, and that is going to be the largest kinetic energy./nBecause those electrons are least strongly bound. So in this neon atom, we've got three different states with three different energies. That is reflected in the fact that we're going to have, in the photoelectron spectrum we're going to have three different kinetic energies for the electrons coming off. So by looking at the photoelectron spectrum you can immediately tell how many energy levels you've got./nAnd, of course, as the kinetic energy goes up, well, that means that the binding energy goes up, the binding energy gets more positive meaning the electrons are less strongly bound. Or, another way to put it, as this kinetic energy goes up this way the binding energy gets more negative this way. The electrons are more strongly bound as that binding energy gets more negative./nBut from this kind of experiment here we can extract what these ionization energies are and we can extract then what the binding energies are. Because of conservation of energy, incident energy of the photon equals the ionization energy plus the kinetic energy. I can rearrange this to calculate the ionization energy. I did that for all of these three features./nHere is the incident energy of that x-ray photon. Here is the measured kinetic energy. The difference between the two is the ionization energy. I solve for that there. And then that ionization energy we know is minus the binding energy. So if the ionization energy is 21.6 eV, the binding energy here for that 2p electron is minus 21.6 eV and for 2s minus 48.4 eV and 1s minus 870.2 eV./nI want you to notice how much more strongly bound that 1s electron is. Then the electrons in the n=2 shell, look at that. That 1s electron is bound by 870 eV binding energies minus 870. Binding energy for the n=2 electrons is minus 48 and minus 21./nWhy is that more strongly bound? Well, that electron is in the n=1 shell, which is much closer to the nucleus where the attractive interaction between that positive charge on the nucleus and the electron is much greater. So this is basically the technique. This is how we calculate those binding energies, or observe those binding energies for the electrons in the multi-electron atom./nWhat I want to do now is I want to start on today's lecture. And you don't have the lecture notes for today's lecture. And there is a reason for that. Oh, and I forgot to tell you to do something very important. I'm going to start on today's lecture. And through this lecture I am going to be asking you some questions./nAnd you're going to have the opportunity to answer, but the way you're going to have the opportunity to answer is that you're going to have to make some paper airplanes. I will ask a question and then I will say launch. And what you have to do is you have to throw the paper airplane to the board. And the first paper airplane that hits the board from that section, well, that section gets a chance to answer that question. And we're going to keep score. And we've got some treats for the winning section. The TAs have some scrap paper and they're going to pass that out. And so you can be making some paper airplanes. Write the number of your section on the paper airplane./nAlso, some of you are not strategically located to his the blackboard. If that is the case, why don't you select somebody from your recitation to be the launcher. They can come down as close as these few stairs and aim at it for your section. OK?/nOK. So I am going to start talking. We're going to talk about the Periodic Table and the trends in the properties along the Periodic Table./nAnd, of course, it's the electron configurations that allow us to understand the structure of the Periodic Table. But it is important to realize that the Periodic Table was first assembled by Mendeleev and other people, not on the basis of knowledge of the electron configurations but on the basis of knowledge of the similar properties./nSimilar chemical and physical properties of the elements. So, for example, lithium, sodium, potassium here, they were all grouped in one column because they were all found to be very soft malleable metals that were very reactive. Helium, neon, argon, they were all grouped in one column because they were found to be very inert, very unreactive./nAnd, of course, now we understand the electron configurations, why these elements have the similar properties. In the case of the alkali metals, lithium, sodium, potassium, we've got that extra x electron, that unpaired electron that makes those metals very reactive. And helium, neon, argon, we've got an inner gas shell configuration that makes those elements very unreactive./nBut by the late 1800s and the early 1900s the similar chemical properties of atoms in a column of a Periodic Table, that really was strongly believed, strongly believed to an extreme. So, for example, it was known that human beings consumed sodium, salt./nIt was known that human beings, our bodies contained sodium ions and potassium ions. Well, if our body has sodium in it and potassium in it and we consume those two elements, why not a little bit of lithium? OK. About 1925 or so a soft drink came on the market./nAnd that soft drink, they wanted to have a lemony flavor to that soft drink. And so how do you get a lemony flavor. Well, you use citric acid. But citric acid isn't really soluble in water so, hey, we've got to make a salt of the citric acid. For whatever reason, a lithium citrate was made./nA lithium salt of citric acid was made. And that soft drink was none other than 7UP. And, in fact, if you look here it tells you that the lithium was touted to give healthful benefits, including an abundance of energy, enthusiasm, a clear complexion, lustrous eyes or lustrous hair and lustrous eyes./nShinning eyes. [LAUGHTER] And so this was on the market until the early 1950s when finally the anti-psychotic properties of lithium were being discovered and the side effects of lithium were being discovered. And the 7UP was then taken off the market, or at least the lithium citrate in the 7UP was removed from the market./nAnd, of course, it wasn't until the early 1970s that lithium was approved as an anti-psychotic drug, because it really is poisonous to the human body in large amounts. And so I really don't know how many individuals had side effects from drinking 7UP at that time./nBut the moral of the story is that even though we're about to talk about some of the general trends in the Periodic Table, don't put any element in your mouth just because it's in the same column as some element that you do put in your mouth. [LAUGHTER] True story. All right. One other property we're going to talk about is the ionization energy. And we've talked about it already but we haven't formally defined it. Let me do that here./nHere you see boron with its electronic structure going to boron plus. The energy change for this reaction is what we call the ionization energy. It's the product minus the reactants. That's the ionization energy. Equivalently, that ionization energy is minus the binding energy of the 2p electron in boron./nThis is a process that is removing the least strongly bound electron. When we remove the least strongly bound electron, the energy that is required to do that is called the ionization energy. And, more fully, it's the first ionization energy. It is the energy to remove the electron from this HOAO, the highest occupied atomic orbital./nOr, the least strongly bound electron. Same idea. This is highest occupied atomic orbital. Now, generally, when we say ionization energy we mean the first ionization energy. We often leave out the word ìfirstî. So whenever you look up an ionization energy, implied in that is that it is the first ionization energy./nThe energy to remove the least strongly bound electron. The second ionization energy, well, that is the energy required to remove another electron. But now we're removing it from boron plus to make boron plus two. And, again, we're removing the next least strongly bound electron. That's the second ionization energy. Equivalently, it is minus the binding energy of the 2s electron in boron plus./nNot boron. And then there is a third ionization energy. Again, now we're taking boron plus two, pulling off the next least strongly bound electron to make boron plus three. That's the third ionization energy. And we can keep going. Boron plus three. Pull out the next electron. Boron plus four, that's the forth ionization energy./nAnd then the fifth ionization energy, taking the last electron off of boron, boron plus four to make boron plus five. That's the fifth ionization energy. So these are our definitions here of the ionization energy. Now, I'm going to switch to the side screen./nAll right. But now here comes the first question. I'm going to show you two reactions here. The first reaction is a boron plus going to boron plus two. We are removing here an s electron./nThe second reaction here is boron going to boron plus. Again, we are removing a 2s electron. And the question is, are these two energies equal. In both cases we're pulling of an s electron a 2s electron. So that's the question. Now, the way we do this is I'm going to move to the side, I'm going to say launch and then Christine and I will try to determine the first airplane to hit the board./nWe will pick it up, and we will ask that recitation section to answer. All right. Ready? Launch. Recitation one, are those energies equal? Answer? It can be a group effort./nHey, you've got a fifty-percent change here. Yes or no? No. They're right. They get a point. OK. You've got to keep score on the board./nAll right. Now why aren't they equal? Hey, big no here. They are not equal because, in this case, this is the ionization energy, the second ionization energy, as we just defined it. Boron plus going to boron plus two, that's a second ionization energy. It's minus the binding energy of the 2s electron in boron plus./nHere, this energy, what this energy is is the ionization energy of the 2s electron in boron, not boron plus. This is equal to minus the binding energy of the 2s electron in boron. This is minus the binding energy of the 2s electron in boron plus. They're not equal. The next question is which one is greater? And so wait a minute. I'm going to get out of the way here./nOK. Launch./nRecitation nine. Over there, sorry. Which one is greater, top one or bottom one? Top one. They are right. Hey, recitation nine gets a point./nYou can put the score on the board. Great. The top one is greater. The top one is greater because the effective charge of this 2s electron in boron plus is larger than the effective charge of the 2s electron in boron. The reason for that is because in boron plus we have fewer electrons. We've got less shielding of the nucleus by the electrons because we have fewer electrons./nSo that's great. But this is really very important for you to understand here. This will be on the lecture notes that I will give to you at the end of the class. Because we might run out of paper, you might want to save those. Now we're going to look at the Periodic Table here./nAnd I'm going to ask this following question here. As we go across the Periodic Table, what we want to know is how does the ionization energy change. So here is my Periodic Table. I'm going across this way. Does the ionization energy increase or does it decrease?/nNow, here is another chance for you to answer this for your recitation section. Launch. Wads don't count. [LAUGHTER] Paper airplanes. Eight. Where is eight? Back there. Hey, OK, eight./nWhat happens to the ionization energy as you go across the Periodic Table? What? Increase. Is that your final answer? You're right. All right. The ionization energy increases. Why does that ionization energy increase? Here is our example. Here is our plot./nIonization energy versus z as you go across. Here is from hydrogen to helium, that's one row, it goes up. Here's from lithium to neon, another row, it goes up. Well, the ionization energy increases because the nuclear charge increases. As you go across the Periodic Table, the nuclear charge increases. The Coulomb interaction increases./nBut there is another part to the Coulomb interaction. And, of course, that other part is the distance. But as you go across the Periodic Table, you're putting electrons into the same shell, to the same principle quantum number shell. And, in general, when you put electrons into the same principle quantum number shell, you are, on the average, the same distance away from the nucleus. And so r is the same./nZ is increasing as you go across. And so, therefore, that ionization energy increase as you go across the Periodic Table. Now, however, you can see that there are some glitches. There is a glitch here between beryllium and boron. Boron is actually a little bit lower in ionization energy that a beryllium. Can we understand that?/nWell, we sure can in terms of the electronic structure. So here is the electron configuration of beryllium, z=4. And then here is the electron configuration of boron, this is 1s, this is 2p, z=5. The bottom line is that it takes more energy to put the next electron here into this 2p state./nAnd the bottom line is that the charge on the nucleus does not increase sufficiently to fully compensate for the energy that is necessary to put that next electron in that higher energy state. So this just doesn't get large enough fast enough to compensate just for the extra energy that is needed to put that electron in the 2p state./nSo we have a little glitch between beryllium and boron. In addition, we've got a little glitch right here between nitrogen and oxygen. The oxygen ionization energy is not as large as you might expect from the increase in the z quantum number. Again, here's the nitrogen./nZ=7, the electron configuration for nitrogen. Here it is for oxygen./nAnd what we had to do for oxygen is that we had to put another electron into a 2p state, a 2p state that already had an electron in it. And there is a great deal of repulsion here between these two electrons in the same state./nAnd, again, the z here, the nuclear charge did not increase large enough or greatly enough to compensate for that electron repulsion. And so the ionization energy is just a little bit lower than it is for nitrogen. That same trend, of course, continues for the other rows in the Periodic Table. Here is the third row./nAnd there is also a glitch between magnesium and aluminum. Magnesium and aluminum are right below beryllium and boron. And a glitch between phosphorous and sulfur, they're right below nitrogen and oxygen. Next question. As we go down the Periodic Table what happens to the ionization energy?/nWait a minute. I'm getting out of the way. OK. Ready? Go. Recitation one. What happens to the ionization energy as you go down the Periodic Table? Decrease. Yes, they're right. Why does it decrease?/nIt decreases, as you go down the Periodic Table, z is increasing, that is true, but as you go down the Periodic Table you're putting electrons into shells that, on the average, are farther out from the nucleus. And so as you go down the Periodic Table it's that distance dependence that dominates the ionization energy./nSo across the Periodic Table ionization energy increases, down it decreases, across its z dependence that dominates because r is constant. As you go down, it is the r dependence that dominates. That is changing. Even though z is changing, r changes faster than z. Great. Now let's talk about another property here. And that other property is called the electron affinity./nIf I take a chlorine atom and I add an electron to it to make Cl minus, the energy change for that reaction is minus 349 kilojoules per mole. That is the chlorine ion is more stable than the chlorine atom./nThis is a reaction that releases some energy. Now, the question is there is a quantity called electron affinity. You need to define the electron affinity. Are you ready to launch? All right. Launch./nFour. Recitation four. You're up there, right? Can you define the electron affinity? What's the electron affinity equal to? I am going to write this. Electron affinity is equal to what? Yes? Answer?/nYes, that's great. But I want a mathematical definition here. EA equals? Negative ie? No. All right. You've got to do another launch. Ready? Launch./nRecitation one. What is the electron affinity equal to? Answer?/nBeep. What it is? No. Next launch. Ready?/nLaunch./nWhat is it? Nine. What is the answer? What is the electron affinity equal to?/nBeep. What?/nYes. Keep going. Not ionization energy. OK. The electron affinity here is minus this energy, right? If you add an electron to an atom there is an energy change. The electron affinity is defined as minus that energy change./nOK. Great game. We didn't get very far. However, from these scores, recitation section one does win. OK. I will see you on Monday.
Tags //
Periodic Trends Elemental Properties
Added: April 16, 2009, 10:32 pm
Runtime: 2153.33 | Views: 18262 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science Electronic Structure of Multielectron Atoms
Chemical Science/n * Email this page/nVideo Lectures - Lecture 9/nTopics covered:
/nElectronic Structure of Multielectron Atoms/nInstructor:
/nProf. Sylvia Ceyer
Tags //
Electronic Structure Multielectron
Added: April 16, 2009, 10:33 pm
Runtime: 3004.80 | Views: 12036 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science - Covalent Bonds - Lecture 11
Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 11/nTopics covered:
/nCovalent Bonds/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 11/nOK. Great./nLet me pick up where we left off on Friday. And that is we were talking about some of the physical and chemical properties of the elements as we go across or down the Periodic Table. And one of those properties that we were talking about was the electron affinity, which I defined for shorthand just EA./nAnd we saw that, for example, if we add an electron to chlorine to make the anion, chlorine minus, that there is an energy change associated with that reaction. And that energy change was minus 349 kilojoules./nAnd what we saw is that the electron affinity is defined as the negative of this energy. So the electron affinity here is minus this delta E. So if you have a reaction that you write with something plus an electron to give the anion here, the change in that energy is this, in the case of chlorine, but the electron affinity is defined as minus that./nAll right. So chlorine we say has an electron affinity of 349 kilojoules per mole. And it is positive. Now, unlike the ionization energy, the electron affinity can be negative. For example, if you take nitrogen and you try to stick an electron on it to make n minus, delta E for this reaction is positive./nWhen delta E is positive it means, of course, that the anion, the product here is less stable than the reactant or the neutral atom. You cannot put an electron onto nitrogen. It won't stay there. It will fall apart./nIt is not bound. And, therefore, nitrogen here, the electron affinity of a nitrogen atom is minus 7 kilojoules per mole. So you can have a negative electron affinity. So nitrogen has a negative electron affinity./nAnd you can understand it in terms of the electronic structure of nitrogen. If you draw the states of nitrogen and put the electrons in the states here, here is the electronic structure of nitrogen, just nitrogen neutral./nBut now if you go and you try to add another electron to the nitrogen it's going to have to go into one of these filled states. There is a repulsion between these two electrons. That repulsive interaction is large enough so that the attractive interaction between the electrons and the nucleus is not great enough to overcome that negative interaction, that repulsive interaction./nAnd, therefore, the electron affinity here is negative or, in other words, this delta E here is positive. So you can understand that in terms of the electronic structure. The other atoms that have negative electron affinities are the inner gases./nHere is a plot of the electron affinities. Here are all the inner gases. They all have negative electron affinities, because you're trying to put an electron in the next shell. That's a higher energy state./nThe charge on the nucleus is not large enough to compensate for that extra energy to promote that electron, to put that electron in that higher energy state. All right. So let's look at what happens here as we go across the Periodic Table to the electron affinities./nAs you go across the Periodic Table, the bottom line is, in general, that the electron affinities increase. They get larger as you go across the Periodic Table. They get larger because the z on the nucleus is getting larger./nThe charge on the nucleus is getting larger. When that charge gets larger the Coulombic interaction between the nucleus and the electrons is greater. And if that's greater, well, then the electron affinity here is going to go up./nAnd it's greater because remember that potential energy of interaction is minus Z times e, the charge on the nucleus times Z over 4 pi epsilon knot r. If Z is going up, this interaction Coulombic attraction becomes greater./nBut at the same time we've got another parameter here, and that's r. And r, as you go across the Periodic Table, is remaining essentially constant because you're in the same shell. So if you're in the same shell, r is about constant./nAnd so the only thing really changing is Z. And so the electron affinity goes up. The same reason why the ionization energy goes up as we go across the Periodic Table, as we talked about last time./nAll right. But now, in general, let's look at going down the Periodic Table here. All right. Fluorine. Chlorine. Bromine. Iodine. Well, in general, the electron affinity actually goes down. And the electron affinity there goes down because r is, in general, getting larger./nYou're putting electrons in shells that are further and further away. Z is also getting larger, but not fast enough compared to r. So, in general, that electron affinity goes down. There are always some glitches, but in general that is the trend./nOK. So then the other property that I wanted to talk about is the atomic radius. And the atomic radius here is plotted on the side. And let's look at what happens as we go across the Periodic Table here./nWell, in general, as we go across the Periodic Table, the atomic radius is going down. The atomic radius is going down because again Z is going up. The charge on the nucleus is getting larger meaning that attractive interaction is getting larger, meaning that those electrons are pulled in closer./nNow, as you go across the Periodic Table again, your r is remaining roughly speaking the same in the sense that the electrons are in the same shell with the same principle quantum number. So, in general, that's remaining the same./nSo that's not changing. It's Z that is changing as you go across the Periodic Table. And that is the dominating factor, the change in Z. The change in Z brings those electrons in closer. And, therefore, the radius actually goes down./nAnd then what about down the Periodic Table, down a column? Well, in this case, as you go down the Periodic Table, again, Z is also increasing. But it's r that is changing faster than Z because you're having electrons in shells that, on the average, are a farther distance away from the nucleus./nAnd that is increasing more rapidly than Z is increasing so, therefore, this radius here is getting larger. All right. So those are the three big trends across the Periodic Table that you should know./nIonization energy and electron affinity increase as you go across, radius decreased. Ionization energy and electron affinity decrease as you go down a column, radius increases. That is something that you do need to know./nOK. Now there is one other concept or quantity that I want to make you familiar with, and that is something called the electronegativity. And the electronegativity is really an empirical concept. We're going to use the definition gave by Mulliken in 1934 as opposed to Pauling's definition./nMulliken's definition is a little bit more straightforward. And the electronegativity is often just labeled chi, and it is given by one-half times the quantity ionization energy plus the electron affinity./nThat is out electronegativity. So the electronegativity here is kind of some average of the ionization energy plus the electron affinity. The electronegativity is some measure of the tendency of an atom to accept an electron or to donate electrons./nSo if the electronegativity of an atom is high that's a good electron acceptor. If the electronegativity of an atom is low, well, that's a good electron donor. For example, if you look at the Periodic Table here and you look at electronegativities, the elements that have high electronegativities, high chi here, are in the upper right-hand corner./nThese atoms have large electronegativities because they have high electron affinities and high ionization energies. These atoms are good electron acceptors. They're good electron acceptors because their electron affinity is high./nThe change in the energy when you add an electron is very large and negative meaning the electron affinity is high. They're good electron acceptors. They're also good electron acceptors because their ionization energy is high./nIt is difficult. You have to put a lot of energy into the system to remove the electron. They're good electron acceptors. On the other hand, if you look at the elements down here in the left-hand lower corner, these elements have low chi./nThey have low electronegativities. They are not good electron acceptors. Their electron affinity is low and their ionization energy is low. So these elements here are good electron donors. Their ionization energy is low./nYou don't have to put in as much energy to pull an electron off as you do for some of the other elements. They have low ionization energy and low electron affinity. All right. So you can already suspect that some of the strongest ionic bonds are going to be made between those elements with high electronegativity and those with low electronegativity./nBecause in an ionic bond, as we're going to talk about, there is this unequal sharing of electrons. So strong ionize bonds are typically made between elements of high electronegativity and elements of low electronegativity./nAll right. And then finally one other concept, or one other definition that I just wanted to make sure everybody was on the same page with is this term here, isoelectronic. Isoelectronic means having the same electron structure, having the same electronic structure./nAll of these atoms and ions have the 1s2 2s2 2p6 electron structure. So nitrogen here. Nitrogen has added three electrons. That makes it minus three to get this electronic structure. Aluminum has pulled three electrons off to get this electronic structure./nThese are isoelectronic. And typically the common ions that are found in nature are ions that have this octet, this inner gas kind of structure to it like the neo structure. So, for example, typically you will see a nitrogen minus three ion./nYou won't see nitrogen minus two because that doesn't have the inner gas configuration. You will see oxygen minus two but you won't see oxygen minus one because that doesn't have the inner gas configuration./nAll right. So common ions in nature are ions that have either added or removed electrons to obtain that inner gas configuration. OK. So those were a little bit of the odds and ends that I wanted to just make sure that we all understood each other about them./nAnd now what we're going to do is we're going to move on, and we're actually going to start talking about what chemistry is all about. And that is the formation of bonds. We're going to take these atoms now and we're going to put them together and we're going to make some chemical bonds./nSo I am going to start to talk about this just in terms of what are the fundamental interactions that are taking place in a chemical bond. So that's what I will do for most of the rest of the hour today, is to talk about those fundamental interactions that are common to all chemical bonds./nAnd then at the end of the hour, I'm going to tell you about one very simple model for bonding which are these Lewis diagrams. And then in the next few days we will look at some more sophisticated models./nWe'll look at molecular orbital theory and we'll look at hybridization. That is the plan. So today just the elementary principles behind chemical bonds, the elementary interactions and a start on Lewis structures./nLet's take hydrogen. That is going to be our prototypical molecule. If we have two hydrogen atoms that are far apart, well, we have the hydrogen nucleus here which is positive and its electron, which we'll call electron A./nAnd they're sort of attached. And way out here is another hydrogen atom. Here is the nucleus and its electron, electron B. And so in the separated atom limit, the interaction that we've got is the electron-nuclear attraction./nThis electron is attracted to this nucleus and visa versa. It's that electron-nuclear attraction that is operable in both of these hydrogen atoms. But now, as these two atoms come closer together, well, this nucleus here is bringing its electron along and this nucleus here is bringing its electron along./nBut what happens is, as they get closer together, this electron that was only attracted to this nucleus, nucleus A, now begins to experience an attraction to nucleus B. And this electron that was attached only to nucleus B experiences an attractive interaction here with nucleus A./nAnd it is that mutual attraction of the electrons for both nuclei that actually is the force, the energy of interaction that brings the two nuclei together, and ultimately a chemical bond is formed./nHowever, at the same time that you now have this additional attraction, this attraction, say, of electron A not only to its original nucleus but to the other nucleus, at the same time as you bring those two together, well, you're bringing the electrons together./nAnd the electrons have like charges and they repel. So, at the same time now, we've got a repulsion, an electron-electron repulsion that is coming into play. And, at the same time to that, we're bringing the two nuclei together, which are both positively charged./nWe've got a repulsion coming up there also. And so the formation of a chemical bond here is an interplay between three very strong interactions, this electron-nuclear attraction, the electron-electron repulsion and the nuclear-nuclear repulsion./nAnd so what we want to take a look at is how those energies actually change. And the components change as a function of the distance between the two nuclei. That's what we are going to look at today./nSo I am going to take two hydrogen atoms here, H, H, and I am going to plot the energy of interaction as a function of the distance between those two hydrogen. So that distance between the two hydrogen here is r./nThat's the distance between the two nuclei. Now, I've changed my definition of r. Up until now we've been talking about r as the distance between the electron and the nucleus, but I just changed it in this discussion of the chemical bond./nIt's the distance between the two nuclei. This is important. Now let me plot this energy of interaction here. And I am going to write this as energy. This is the energy of interaction. It's going to be in kilojoules per mole./nAnd I am going to plot it as a function of r, this distance between the two nuclei. And what I am going to find, this is going to be zero of energy here, is that way out here where the two hydrogen atoms are separated, this energy of interaction is going to be minus 2624 kilojoules per mole./nSo this is hydrogen plus hydrogen. Hydrogen atoms infinity separated. But now I am going to bring those two hydrogen atoms together. And what happens is that the energy will go down. The energy of interaction will go down, it will keep going down until some point, and then it will start going up./nAnd that energy of interaction will be actually at some value r here greater than what it was in this separated atom limit. Now, everywhere where this energy of interaction is lower than the separated atom limit -- Everywhere along these values of r we have a chemical bond./nThe two hydrogen atoms are bound because their energy of interaction is lower than that of the two separated hydrogen atoms. Where it is the lowest, where that energy of interaction is the lowest is the equilibrium bond length./nThat's what defines the bond length, is the value of r at which that energy of interaction here is the lowest, is the most negative. That's the equilibrium bond length. In the case of H2 that bond length turns out to be 0.4 angstroms./nEverywhere here, where that energy of interaction is lower than that of the separated hydrogen atoms, from here to here, we call that the attractive region of the potential energy of interaction. We call that the attractive region, because everywhere here, from here to here two hydrogen atoms are bound./nThey are lower energy than that of the separated hydrogen atoms. So, in other words, they are bound if they are at this value of r. They're bound if they're at this value of r. It's just that they are most strongly bound at the equilibrium bond length./nSo that's how you read the curve. This well here, if you will, we call this sometimes a well, that's the attractive region of this energy of interaction curve. Sometimes we call it the potential energy of interaction./nAnd then another important definition here is the change here from the bottom of this well to the separated atom limit, as you measure it from the bottom to the separated atom limit that energy change I'm going to call delta e sub d./nThis is the bond association energy. This is how much energy it's going to require to dissociate the H2 molecule if it's sitting in its equilibrium position from here to here. That turns out to be, in kilojoules per mole, 432 kilojoules per mole./nThat's the bond association energy. But you also notice here something a little peculiar in the sense that you can bring these two hydrogen atoms in. And if you bring them in too close, that is if you start to push them in closer than their equilibrium bond distance the energy of interaction goes up./nAnd you can keep pressing them in. And the energy of interaction will go even further up. In other words, will increase more as you push those two hydrogen atoms in. The energy of interaction can get above that of the separated hydrogen atoms./nAnd it's this region of the potential energy of interaction that we call the repulsive region. It's repulsive because if you push those two hydrogen atoms closer than about this point right here, those two hydrogen won't stick together./nThey're even closer than the bond length, but they're not going to stick together because their energy of interaction is greater than the separated hydrogen atom limit. So that is, in general, what the energy of interaction looks like for every chemical bond./nBut this curve here is really given by the competition and the interplay between these three interactions that I started talking about right here. And so I want to try to decompose this curve into those three interactions./nAnd that is what we're going to do now. We're going to try to explain why that curve has the shape that it actually has. I started out saying that this energy of interaction, I will just call it energy of I here, was really the sum of three interactions./nOne of those interactions was the nuclear-nuclear repulsion between the two nuclei. That's one. Another one of those interactions was the electron-nuclear attraction -- -- between the electron and both nuclei, or between both electrons and both nuclei./nAnd the finally, the third, is this electron repulsion between the two electrons as we bring the two hydrogen atoms closer together. So those are the three components. Now, what I want to try to do is I want to try to figure out an r dependence for each one of those components./nI want to see how each one of those components change with r. And then when I add that up, I should get something that looks like that. OK? All right. So how are we going to do that? Well, first of all, I am going to realize that with a nuclear-nuclear repulsion, what is that r dependence going to look like? You want to guess? Coulomb interaction, right? Coulomb interaction between like charges./nThat's what that r dependence is going to look like. So that's e squared for the hydrogen atom, the charge on the nuclei. Each hydrogen atom is e over 4 pi epsilon knot times r. In the case of the nuclear-nuclear repulsion right here, I've got a very good handle on what that r dependence for that interaction energy should look like./nHow come I ran out of board here? Oh, wait a minute. All right. Let me draw that. So I have the energy of interaction here. And I've got a zero of energy. And so I'm drawing a one over r dependence there./nWell, one over r looks like it starts at infinity and drops off to zero for very large values of r. So this is my nuclear-nuclear repulsion. That is this dependence right over here. I have one of the components, but now what about the electron-nuclear attraction and the electron-electron repulsion? Well, it turns out that I have no simple way to predict the r dependence for the electron-nuclear attraction or the electron-electron repulsion./nI have no simple way to do that without doing a sophisticated calculation. And, in fact, I don't even have a simple way of doing that if I want to sum these two terms. These two terms are really the electron interactions./nThese two terms involve the electron-electron repulsion, electron-nuclear attraction. This one didn't have any electrons in it. So I have no simple way to do that. However, what I can do is that I can evaluate the sum of these two energies at two extremes./nI can evaluate the sum of these two energies when r is infinity way over here, and I can evaluate the sum of those two terms when r is at zero way over here. So I am going to have two points, and then I am going to interpolate between those two points to get my r dependence./nThat's what I'm going to do on my graph over there. So let's do that. I am going to erase this here. Let's start by looking at what that energy of interaction is at r equal infinity. At r equal infinity, what is the electron-electron repulsion equal to? Zero, because the electrons are very far apart./nThere is no interaction there. When r is equal to infinity, what is the electron-nuclear attraction? I'm sorry? What is the electron-nuclear attraction? I'm over here. When r is infinity, what is the energy of interaction for the electrons in the nuclei? It's not zero because when the two hydrogen atoms are separated, in each hydrogen atom the energy of interaction is? How about the binding energy of an electron to a nucleus, right? It is the binding energy of the electron to the nucleus./nThat's the binding energy of the electron in the ground state. It's the binding energy of the 1s electron. Make sense? Does this make sense to you? No it doesn't. No. OK. What's confusing? You don't know./nDo you understand what I am plotting here as a function of r, the distance between the two nuclei? OK. When the two nuclei are very far apart -- Right over here they're really far apart. There is no electron-electron repulsion./nBecause each electron is attached to each nucleus and they're too far apart for there to be any repulsive interaction. That makes sense, right? But when they are far apart here the electron-nuclear attraction, between this electron and its nucleus here, that electron-nuclear attraction, that energy of interaction is the binding energy of the electron to the nucleus./nIn the case of the ground state hydrogen atom it is the binding energy of the 1s state. Does that make sense? Yes? No? Good. But we've got two hydrogen atoms so there is a two in front of this. We've got two hydrogen atoms so there is a two in front of that./nAnd now you know that the binding energy of an electron to a nucleus is minus 2.18 times 10 to the minus 18 joules, right? Yeah, you know that. I am going to turn that into kilojoules per mole instead of joules per molecule./nWhen I turn that into kilojoules per mole, it is 1312 kilojoules per mole. If I multiply that by two, I am going to get 2624 kilojoules per mole. And so way out here at r equal infinity I've got one point minus 2624 kilojoules per mole./nThat is where that number came from in this original graph. Do you understand that? This is important because these are the interactions present in all chemical bonds. So we've got that. Now we're going to estimate what the sum of these two terms are at r equals zero./nAt r equals zero we've got the electron-nuclear attraction and we've got the electron-electron repulsion. How are we going to do this? Well, at r equals zero, what we've got are two hydrogen atoms with the nuclei right on top of each other because that's what r equal zero means./nThere is no distance between the two nuclei, right? So we've got two protons right on top of each other. And, as far as we're going to be concerned here, if you've got two protons right on top of each other that looks like a helium nucleus./nIf we've got two protons right on top of each other at r equals zero, Z is going to be plus two. That is going to look like a helium nucleus. This is a thought experiment. We're taking two hydrogen and we're putting them right on top of each other./nSo you've got something that looks like a helium nucleus, Z=2. And now, because r is equal to zero, we've got two electrons around that helium nucleus. So all of a sudden what we've got here is something that looks like a helium atom./nThis looks like a helium atom in this thought experiment. How can I estimate the sum, not these individuals but the sum of these interactions in the helium atom? In the helium atom we have the electron-nuclear attraction, the attraction between this electron and the helium nucleus, this electron and the helium nucleus, and we've got the repulsion between these two electrons./nHow can I estimate that? Well, experimentally I can estimate that by taking the first ionization energy, making that minus, plus minus the second ionization energy. That will be my total energy of interaction as far as the electrons are concerned./nSo I go and I look up the first ionization energy of helium. Remember the first ionization energy was the energy required to pull off the first electron? I find that number. The binding energy is minus that ionization energy so that's why I put that minus sign there./nI do that, and that removes one electron. And now I want to know how much is this electron bound to the nucleus. I go up and I look up my second ionization energy for helium where I solve the Shrˆdinger equation for a one electron atom./nI look that up. That's minus the ionization energy. It turns out that the sum of those two is minus 7622 kilojoules per mole. Does this make sense? The electron-nuclear attraction plus the repulsion./nI cannot separate those two terms, but I know what they are experimentally as a sum because I go and I measure how much energy is required to pull the first electron off, add it to the energy required to pull the second electron off./nThat's totally the electron-nuclear attraction plus the electron-electron repulsion. That's what that is. And I have to make it negative because the binding energy, the energy interaction is minus the ionization energy./nSo way over here on this plot I've got another point for r equals zero. That is minus 7622 kilojoules per mole. And so now what I'm going to do is I am going to just draw a line here between the two./nI just interpolate it because I don't know what else to do. I don't know how to get that energy of interaction in a simple way as a function of r in any other way. But now what I've got are the three components./nHere is one, the r dependence. Here is my approximation for the r dependence of the sum of the other two components. I am going to add them up. Because my total energy of interaction I said was the sum of those three./nAnd when I add them up, well, what I am going to get, if I add this curve to that curve, I'm going to get something that looks like that. This is going to bring it down. This goes to infinity so this will go high up to infinity here./nI am going to get a potential energy of interaction that looks something like that. The point of all of this was to illustrate that a chemical bond is really a result of the competition between the electron interactions./nThe electron interactions are this green line here. It's a competition between the electron interactions, which is always negative. Even though you have an electron-electron repulsion here, which is a repulsive interaction, the overall energy of interaction is negative./nIt's attractive. The electron interactions overall are attractive. They're negative. So this chemical bond is a competition between the electron interactions, which are attractive, and the nuclear-nuclear repulsion, which is always repulsive./nThis was always positive. It's always repulsive. And what you can see here is that there is some optimal distance which ends up being the bond length where the total energy of interaction is a maximum negative number./nWhere the total energy of interaction is the greatest. In other words, what you have to do is you're going to make a chemical bond. You have to bring the two atoms in close enough so that the electron attractions are present, which bring the two nuclei in./nBut you cannot press them so close together such that the nuclear repulsions take over. So there is some intermediate distance here where you have enough electron attraction, but you don't push them so close that the nuclear repulsion takes over./nAnd it is that optimal distance here that is the equilibrium bond length. Now, there is one other very important point. And that is that what we often do is we shift this zero of energy when we talk about a chemical bond./nThis zero of energy right now is 2624 kilojoules above the energy of the separated hydrogen atoms. But we already saw that this energy of interaction is the energy of interaction between the electron and the nucleus in the separated hydrogen atom limit./nWhen we talk about a chemical bond, we really want to know what the energy of interaction between the two hydrogen atoms is. And so it is useful for us to take for us to take this zero of energy here and just shift it down and set it here, make this the zero of energy./nNow our zero of energy is when the two hydrogen atoms are separated from each other. That is just the convention. It is often useful to talk about chemical bonds when you set the two atoms. When they are far apart and you set that energy of interaction equal to zero./nSee you on Wednesday.
Tags //
Covalent Bonds
Added: April 16, 2009, 10:40 pm
Runtime: 2831.67 | Views: 14232 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.
Chemical Science - Breakdown of Octet Rule - Lecture 13
Principles of Chemical Science/n * Email this page/nVideo Lectures - Lecture 13/nTopics covered:
/nBreakdown of Octet Rule/nInstructor:
/nProf. Sylvia Ceyer/nTranscript - Lecture 13/nThe goal is to count up all of the valence electrons that you have in a molecule and then distribute those valence electrons so that between each two atoms there are at least two electrons./nAnd then what you do is you take the rest of the electrons and distribute them around the molecule so that each atom has an inner gas configuration around it. That's usually an octet, unless you're dealing with hydrogen. That's the main idea. And so what that means is that you have to know what those valence electrons are./nAnd so that is something that you should get used to knowing so you could just really write that down immediately. But we also saw last time that a very critical concept was this concept here of formal charge. Formal charge is a measure of how much an atom has gained or lost an electron when it has formed a bond in a particular structure./nAnd we saw how this idea of formal charge was really critical in being able to determine what the lowest energy structure was. In fact, what was the lowest energy skeletal structure? Often times, when you start out, you don't know what atoms are connected to each other. You have to take a guess. You take a guess. You put out the Lewis structure./nYou draw out the Lewis structure and then you calculate the formal charge. And if you find on that Lewis structure that any atom has a formal charge, a minus two or a plus two or minus three or plus three, that cannot possibly be the lowest energy structure. And then you start again. You find another skeletal structure, draw out the Lewis diagram, calculate the formal charges./nAnd you keep doing that until you find a skeletal structure that gives you the lowest set or the lowest absolute values of formal charges. This is a very important concept. That's how you do it. Now, we also saw last time that we were able to draw a couple of different skeletal structures were the set of formal charges was the same./nExcept that in those two different Lewis structures, one structure had a formal negative charge on an oxygen and the other one had it on the nitrogen. In that case, we want to always make sure we put the negative formal charge on the most electronegative element. And then, finally, in our discussion of formal charge, we were talking about this ion here, NO3-./nAnd this formal charge concept helped us to understand when we had a resonance structure. For example, we did a Lewis structure that looked like this. And we put this double bond here between one nitrogen and one of the oxygens, but we realized we could have also put it between this nitrogen and oxygen and we realized we could have put it between this oxygen and this nitrogen./nAnd, of course, in all three cases we've got the same set of formal charges. They look identical. So what happens in this case? Well, when you've got this situation where it looks like you've got three different structures and the formal charges are the same, well, this is a hint that you have a resonance structure. That is that these two electrons here, these two extra electrons are not sitting between just one nitrogen and an oxygen./nBut rather these two electrons are delocalized over all three bonds. That is to say these three bonds, nitrogen-oxygen, nitrogen-oxygen, nitrogen-oxygen are all equivalent. It is not the case where one of the bonds is a double bond and the other two are single bonds. Rather, those extra two electrons are distributed equally over all three bonds./nAnd so each one of these bonds kind of looks like a bond and a third. It's a little bit shorter than a single bond and a little bit stronger than a single bond, but not as short as a double bond and not as strong as a double bond. When you have this situation of three sets, three different structures, three different Lewis structures but same set of absolute values, that's a clue you've got a resonance structure./nOK? Yes?/nNo, the lone pairs here are not. They actually reside, they're most close to the actual atom that they're shown. It's only the bonding electrons that exhibit this delocalization./nAll right. Now what we want to do today is I want to show you some exceptions to the octet rule. There are always exceptions. And we started out saying that these Lewis diagrams and the octet rule, that worked 90% of the time. Now I want to show you the other 10% when it actually doesn't work. And so here is the first exception when it doesn't work./nIt doesn't work when you have an odd number of valence electrons because these Lewis diagrams are based on the idea that a bond shares, a bond is composed of two electrons, and those two electrons are shared between the two atoms. And so if you've got an odd number of valence electrons this whole idea breaks down. For example, the methyl radical, CH3 dot./nA methyl radical has an odd number of valence electrons. It has seven valence electrons. It is because it has that one unpaired electron that it's actually really very reactive. And so if you try to use your Lewis rules that we had on this kind of situation where you've got an odd number of valence electrons, everything really just breaks down./nSo if you're given a structure to draw and you've got an odd number of valence electrons forget it. You really cannot use the octet rule and then the Lewis diagrams to do that. You need a more sophisticated scheme for looking at the bonding of molecules which have an odd number of valence electrons. And we're going to look at some of those more sophisticated schemes in a couple of days or so. So that's one exception./nBut here comes a second exception, and this is an exception to the octet rule. The octet rule is going to break down, but we are still going to draw a Lewis diagram. And I will show you how. The octet rule is going to break down for these elements in group 13. The octet rule is going to break down for boron, aluminum, gallium, indium in the group 13./nYou come to a problem where you've got to draw a Lewis diagram for a group 13 element. Do you know what should happen in your mind? Buzzers ought to go off, buzz, buzz, buzz meaning there's going to be an exception here. I mean this. Really, if you see boron, aluminum, you're on heightened alert here. Something unusual could happen. Let me explain this. Suppose we are writing the Lewis structure for BF3, we need the skeletal structure first. Well, I said last time that the fluorines, they're just almost always terminal atoms. Good guess. Put the boron in the center. Now let's count up the number of valence electrons./nWell, we have four atoms here. Each of the three fluorines are bringing in seven valence electrons and the boron is bringing in three. We've got a total number of 24 valence electrons here. I just drew them out. Now we want to count up our step three here, the number of electrons that we would have to have if each one of these atoms had an octet around it. So we've got four atoms. Each one wants eight./nSo we would have to have 32 electrons. To calculate the number of bonding electrons in step four we subtract the number of electrons that we'd have to have for an inner gas configuration from the number of valence electrons that we do have. And that is eight. And what I did last time is I put a square here around the valence electrons that are going to be bonding electrons./nAnd our next step in the Lewis diagram said we're going to assign those bonding electrons, two to each bond. Let's do that. Well, we just did it. Here is two, here is two, here is two. We used up six of the bonding electrons. And our next step says do we have any remaining bonding electrons. Well, yeah, we do. We've got two bonding electrons here that we haven't used./nAnd we said last time in this case what we usually do, or what we do is that we assign those electrons so that we have multiple bonds. We have a double bond. For example, we're going to choose one of these boron-fluorine bonds and put in another two electrons so that we have a double bond between the boron and the fluorine. That's what our rules said last time, so let's follow them for a moment. So we did that. Now we've used up all of our bonding electrons./nDo we have any valence electrons left? We sure do. Gobs of them. We only used eight of them for the bond so we've got 16 valence electrons. That means we're going to have to make eight lone pairs. And we distribute them around each atom in the molecule so that each atom has an octet. So let's do that. Here we've got eight around fluorine, eight around this fluorine, there's eight around the boron and there is eight around the fluorine./nEverything looks normal. Everything looks great. Now let's calculate the formal charge. That is something else we've got to check. Formal charge is number of valence electrons minus the number of electrons that are lone pairs minus the number of bonding electrons divided by two. Let's calculate that for boron in this structure./nSo we said boron has three valence electrons. How many lone pairs does boron have in this structure? How many little pairs? None. They're all bonding electrons. How many bonding electrons does boron have? Eight. Eight divided by two is four. The formal charge on this boron is minus one, so we're going to put a minus one right there./nAnd then if you proceed to calculate the formal charge on this doubly bonded fluorine right here, you would find that that formal charge was plus one. And if you go and you calculate the formal charges on the singly bonded fluorines, you would find that that is zero. So I will put a zero and a zero there. And now, remember, last time we said that the sum of those formal charges has to equal the overall charge on the molecule./nIf it doesn't you've done something wrong somewhere. And so I just summed them up. That sum is zero. The overall charge on BF3 is zero. We did things correctly. But now when you look at this you say, well, this looks like NO3- in the sense that I could have taken these two electrons and put them in this bond to make that structure. If I did, I'd have the same set of formal charges./nOr I could have taken those two electrons and put them right here like that. If I did so, I would still have the same set of formal charges. Look, this looks like one of these resonance structures that I just told you about. That's what it looks like. Why not resonance? Well, why not? Because this beeper is going off in your head, beep, beep, beep, this is boron./nBoron is an exception. Let me show you how it is an exception. Experimentally, if you look at these boron-fluorine bonds, you would not see that there would be one double bond and two single bonds. You would not find a boron-fluorine bond that looks like a double bond and two that look like single bonds./nYou would also not find that these three bonds were a bond and a third like in NO3-. Experimentally, you would find that these boron-fluorine bonds all have the same length but they are typical of a single bond. Unlike in NL3- where it was a bond and a third, these boron-fluorine bonds all look like single bonds in terms of their lengths, in terms of their strengths./nVery different than NL3-. Given that experimental observation, what are we going to do? Well, we're going to write a structure here where we're going to give every atom in that structure an octet except for the boron. So what did I do?/nI took the extra two electrons here, removed it from the boron-fluorine bond and gave it just to the fluorine so that every fluorine or every atom in this molecule has an octet, except for this outlier boron. Still got the same number of electrons, everything is fine, but I moved these electrons from here to the fluorine./nLet me calculate the formal charge here. If I do that, I find that the formal charge on boron is zero now instead of minus one. I find that the formal charge on this fluorine is zero, this fluorine is zero, and this fluorine, hey, that's zero. I've got a structure with all zero formal charges. That is awesome. [LAUGHTER]/nThe octet rule just broke down here. And that is the case for the elements in group 13, or that is often times the case for the elements in group 13. In BS4-, for example, the octet rule doesn't break down. But in BF3, BCL3, aluminum trichloride same thing./nThe group 13 elements are octet deficient. So that's an exception that you have to know about. And, in fact, this is the structure. Experimentally we can tell that. And it's the lowest energy structure. We've got a set of zero formal charges. So that's group 13. That is our second exception./nThis just repeats that. Great. Now here is our third exception. So we've got an exception now where we don't put an octet around some atoms. And now this is the opposite case. The third exception is where we're going to put more than an octet around an atom. We're going to call this valence shell expansion./nAnd the example we're going to use is phosphorus pentachloride. Let's draw the Lewis structure first, and then we will see how our rules are going to kind of break down. For phosphorus pentachloride, let's put the phosphorous in the center because the chlorines are usually terminal. Not always but usually. So let's start there./nWe do that. Let's calculate the number of valence electrons. Well, fluorine, it brings in seven valence electrons. There are five of them. Phosphorus, it brings five valence electrons into the party. We've got 40 valence electrons. How many electrons would we have to have if we had an inner gas configuration around each atom? Well, we've got six atoms. Six times eight is 48./nSo what do our rules say about the number of bonding electrons? Well, our rules say that we've got eight bonding electrons because 48 minus 40 is eight. Well, that's great. Eight bonding electrons, we can make four bonds. But we've got a problem. You can see already that we're going to have to make at least five bonds so we've got a problem. Our kind of formula here for writing these Lewis structures broke down./nIt's clear we're going to have to make ten bonds, but in our procedure here it let us make only four bonds. So what are we going to do? Fudge. Good. That's exactly what we're going to do. We're going to fudge. We're going to forget our rules. We're going to draw five bonds, each one to chlorine. So now, of our 40 valence electrons, ten of them have been used as bonding electrons./nThat means we've got 30 valence electrons leftover. We're going to have to distribute them around the molecule so that each atom, except the phosphorus, has an octet around it. We will do that. Here are six for that chlorine. Now we used another six, 12 for that chlorine./nAnother six for that chlorine, 18. Another six for that chlorine, 24. Another six for that chlorine, 30. We just used them all up. Let's calculate the formal charges. The formal charge on phosphorus is number of valence electrons on phosphorus, which is zero. Number of lone pairs on phosphorus, which is zero. And number of bonding electrons divided by two on phosphorus. Well, there are ten bonding electrons./nTwo, four, six, eight, ten divided by two, that's five. Formal charge on phosphorus is zero. And now if you go and you calculate the formal charges on the chlorines, they are all zero. And we've got another awesome looking structure here, a set of zero formal charges for phosphorus pentachloride. That is very nice except for the fact that we've got more than an octet around the phosphorus./nThe phosphorus has what we call an expanded shell. And that is the case, that will be often the case for elements which have their outer most electrons in a shell where the principle quantum number is three or greater. Those elements have empty d states./nEmpty d states that can accommodate more than eight electrons that can accommodate more than an octet. And phosphorus is one of those elements. So when you start to get to the larger elements like phosphorus, like the next example iodine that I am going to show you, we can put more than an octet around those larger elements. Let's do another example here with this valance shell expansion./nHere is the IF4- ion. How do you draw, first of all, a skeletal structure? What is a good guess for a skeletal structure here? Well, chlorines are always terminal. Let's put them on the outside and the iodine in the middle./nIs there a question over there? Can I help you out? Any questions right now? OK. Let's try it. Let's count up the number of valence electrons. Well, we've got one, two, three, four, five atoms. And they are halogens. Halogens bring in seven valence electrons. Five times seven is 35. But, and this is important, we've got an extra charge here./nThis is an ion. It is minus one. And so we're going to have to add one to the number of valence electrons. We've got 36 valence electrons. Now, the number of electrons of each had an octet so that would be 40 because we have five. Five times eight is 40. According to our rules then, the number of bonding electrons is 40 minus 36 which is six./nWhich is four. [LAUGHTER] It's four. But what do we need? We need eight bonding electrons because we've got to make four bonds. Here again we have a breakdown in our rules. Something is wrong. We are going to have to fudge, as somebody said. We're going to ignore our rules. We've got to make eight bonds. Oh, jeez./nWe've got to make four bonds so we need eight electrons. Let's make them. There they are. So we used eight of the valence electrons as bonding electrons. 36 minus eight is 28. We've got 28 remaining valence electrons or 14 lone pairs. We're going to distribute them around that fluorine. There are six, that fluorine, there is another six, and that's 12. That fluorine is 18. This fluorine is 24./nWe just used up 24 of those valence electrons, but we haven't used them all. We've got four valence electrons remaining. Where are they going to go? Well, where we are going to put those four remaining valence electrons are around the iodine right there. We're going to give them to the iodine, and the iodine is going to have two lone pairs./nSo the iodine here has four more electrons around it. And we can do that again because the iodine has got some empty five d states that can accept these electrons, and it does. Everything has got an octet here except for the iodine. Let's check the formal charges and make sure we did everything correctly./nCalculate the formal charge on iodine. Well, number of valence electrons, seven. Minus the number of lone pairs. Look at how many lone pair electrons we have on the iodine, two, four. We've got four lone pair electrons on iodine. Minus one-half the number of bonding electrons on iodine. Well, we've got eight bonding electrons. Here they are, two, four, six, eight. These red ones don't count. They are the lone pairs./nEight over two is four. The formal charge on iodine is minus one. If you go and you calculate the formal charges on fluorine, they are all zero. Some of those are minus one. That is indeed the overall charge on this iodine tetrafluoride. So we did it right./nHere is another case where there is an octet around each one of the atoms, except for that larger atom, the iodine, which has actually two, four, six, eight, twelve electrons around it. Yes?/nNo, these aren't d electrons necessarily. These are in empty states here. There is plenty of room even to put some more in the case of iodine. We saw that these Lewis diagrams, the octet idea works 90% of the time, but three exceptions. An odd number of electrons?/nForget it. You cannot use it. We're going to find some more sophisticated models for bonding. It doesn't work on group 13. Group 13 elements often have less than an octet. And then, finally, if you get to the heavier elements like iodine, like phosphorus that we looked at, like chromium is one example in the notes that I didn't work through./nBut you will work through that in recitation. You've got some empty d states. You can put more than an octet around those heavier atoms. So that is what I wanted to say here about the Lewis diagrams. And next, on Friday we're going to start looking at a little bit more sophisticated model for chemical bonding, which is molecular orbital theory./nBut right now what I want to do is I want to talk about one other kind of classical model for chemical bonds. It is a model that works only for a very ionic bond like sodium chloride. That is what we're going to talk about here./nAnd, in particular, it's a model that is simple but accurate in terms of giving us a physical picture of actually how this chemical bond forms. Let's talk about it. We're going to talk about the formation of a bond between a sodium atom and a chlorine atom. How does this happen? Well, we've got sodium and chlorine coming together./nWhat happens here is this sodium ejects an electron and its spheres the chlorine, and that electron now is stuck on the chlorine. And so now the chlorine is Cl-. It's pretty big. Sodium is Na+. It's small. And once that happens that sodium just ropes that chlorine right in. It just pulls it right into it./nIt is called the harpoon mechanism. Now, once that electron jump happens of course these two ions come together. What is this rope in between the sodium plus and the chlorine minus? Well, that rope is the Coulomb interaction, right? Because once that electron has jumped from sodium to the chlorine, we have a positive charge and a negative charge./nAnd they are attracted. And they just zoom right in together until you get to the bond length and they form a chemical bond. That is literally what happens. The sodium ejects an electron, that jumps to the chlorine, and then the two just zoop right into each other and form a chemical bond called the harpoon mechanism./nThis is a mechanism here that was really shown experimentally by Dudley Herschbach here at Harvard in the Chemistry Department, John Polanyi in Toronto and Yuan Lee in UC Berkeley. And for this mechanism and for many other dynamics of chemical reactions they got a Nobel Prize in 1986./nAnd Yuan Lee over here was actually by thesis advisor at Berkeley. This seems like a very peculiar kind of way for a chemical bond to form but, in fact, it is accurate. Let me talk about the energetics here of this process because that will help in trying to understand physically really what is going on in this bond formation./nBecause the first thing you're saying is, well, when that electron jumps that costs energy. We know that. We know that for a sodium atom to remove an electron here that there is an energy cost, delta E. That energy cost is what physically? The ionization energy./nThat's the ionization energy. That's 496 kilojoules per mole. But it is also true that once that electron gets in the vicinity of chlorine, the chlorine grabs it. That is the chlorine plus the electron here. When that happens some energy is released to make the chlorine minus. That energy, delta E, is minus the electron affinity./nThat was one of the definitions that we worked on a few days ago. And minus the electron affinity there is minus 349 kilojoules per mole. So you get some energy back when that electron attaches to the chlorine./nBut, overall, if I sum things up here with a sodium gas phase atom and a chlorine gas phase atom going to Na+ plus Cl-, the delta E for this reaction here overall is still positive 147 kilojoules per mole. You still have to put some energy into this system to make this reaction go. And, of course, this delta E here, I used the number 147. I added these up./nBut delta E also can be written here as the ionization of sodium minus the electron affinity of chlorine. But it's still uphill to get the electron to go from sodium to chlorine. However --/n-- the sodium and the chlorine now, once they are two ions and they come together, we're going to have some energy released because we're going to form a bond. Na+ plus Cl- going to NaCl, well, the delta E for that reaction is minus 592 kilojoules per mole./nThen overall I am going to add up this reaction to that reaction, so these are going to cancel. We have sodium gas phase plus chlorine gas phase to make sodium chloride. That is the initial reaction we were looking at, sodium and chlorine to make a sodium chloride molecule./nOverall, that delta E is minus 445 kilojoules per mole. Overall, the action is releasing energy. And that is good but things still seem a little strange, right? It still seems a little strange that this sodium is ejecting an electron and that chlorine is grabbing it and then they come together. This ejecting of an electron is a little bothersome so let's look a little more carefully at what is going on./nAn energy level diagram. Those are the energetics. And now I am going to put those energetics that I just described onto a diagram to try to make it a little bit more realistic for you. What I drew here is the energy of interaction for sodium plus a chlorine atom./nThis is the same shape that I drew for two hydrogen atoms. It's the same shape because whenever two atoms come together to form a bond, the energy of interaction looks like this. This is a general phenomenon. Way out here the two atoms are separated. The energy of interaction is zero. As they come together, there is an attractive interaction. The energy gets lower./nIt continues to get lower until we get to some value which is the bond length. It is at this point, this value of r that you have the most stable configuration. This is the chemical bond. You push them closer together. The energy goes back up. And then this well depth here, from here to here or backwards from down here to up here./nFrom down here to up there, that's the bond association energy delta E sub d. In this drawing, I reversed it. I went from here to here. It is minus delta E sub d. It's minus 445 kilojoules per mole. That's this number that I calculated right here. This is the bond strength, 445 kilojoules per mole. That's the bond strength in the sodium chloride molecule./nThat's how much energy is going to be required to take sodium chloride and pull it apart into the neutral atom sodium and the neutral atom chlorine. That is physically what that number is. But now what did I say earlier? I said that sodium ejects an electron which ends up on the chlorine./nAnd if that is the case, that is if that sodium ejects an electron that ends up on the chlorine and it does it when the sodium and the chlorine are far apart, that's going to require 147 kilojoules per mole. That is what we calculated there. That is this number. That is 147 kilocalories uphill./nSo if sodium and chlorine are really far apart, that is how much energy it is going to require to pull that electron off of sodium and put it onto the chlorine. This is IE, ionization energy minus the electron affinity. I said that that happens when it is far apart, but now the sodium ion and the chlorine ion come together. They come together to the bond length./nAnd at the bond length they form this chemical bond. And when they form this chemical bond, well, then what we have released is this much energy much 592 kilojoules per mole. Now, where did this number come from? Well, that number comes from the following simple model./nThat number comes from the potential energy of interaction between a bare plus charge and a bare minus charge at r equal 2.36 angstroms. This is the potential energy of interaction for a plus charge and a minus charge, so it's minus e squared. R here is this bond length, 2.36. If you evaluate that at r point, 2.36, you will get 592 kilojoules per mole./nSo what did I do here? I treated sodium ion and chlorine ions like two bare point charges. I forgot about the fact that sodium here has got other electrons. I forgot about the fact that chlorine here has got other electrons./nI just approximated it s2 point charges and used the Coulomb interaction between a bare plus charge and a bare minus charge to get this energy, 592 kilojoules per mole. That is where that comes from. So when the sodium and chlorine come together to this bond length, well, then they form a bond and this much energy is released within this model here./nSo we're beginning to understand what all these numbers are and physically what is going on, except maybe what is still bothering you is the fact that it still look like, in order for this reaction to go, that I've got to put in 147 kilojoules per mole into the action before I am going to get any energy back. It kind of looks like there is a barrier to this reaction from what I've told you so far./nBut the answer is there isn't because when the electron jumps is not when the sodium and the chlorine are infinitely far apart. But when the electron jumps is when the sodium and chlorine are right here at this value of r star. Why right here?/nWell, it happens right here because of this. This blue line here, see this blue line? What that is the Coulomb energy of interaction as a function of r between two point charges, plus one and minus one. So way out here when r is very large that energy of interaction for these two ions is zero./nBut as these two ions come closer together that energy of interaction becomes more and more negative. There is a one over r dependence here. And that is what that blue line approximates. At some point that Coulomb interaction energy crosses this black curve here which represents the interaction energy between a neutral atom and a chlorine atom./nRight here the Coulomb interaction energy is the energy difference between up here to down here. Right here this is the Coulomb interaction energy minus E squared four pi epsilon knot at r star now, not equilibrium distance./nAt r star where the electron jumps. Right here, this Coulomb energy of interaction equals this energy difference between the two separated ions and the two separated atoms. This energy difference here measured from here to here is minus the ionization energy minus the electron affinity. So right here this electron can jump and it doesn't cost us any energy./nBecause the Coulomb interaction has already set in. Right here that Coulomb interaction energy is equal to this energy difference. That is when the electron jumps, right here. And then it is at that point that the sodium and the chlorine are accelerated together up to the equilibrium bond length form of bond and you have the sodium chloride molecule./nLet's calculate what this value of r star is. At what value of r does this electron actually jump? Well, we can do that. This is minus e squared over 4 pi epsilon knot r star. That is going to be equal to minus the quantity ionization energy of sodium minus the electron affinity of chlorine./nLet me rearrange this here. I am going to solve for r star. R star is equal to e squared over four pi epsilon knot times the quantity ionization energy of sodium minus the electron affinity of chlorine./nR star is equal to e squared. E squared is 1.602 times ten to the minus nineteen Coulombs squared over four pi epsilon knot, you can look up epsilon knot, times this difference in energy./nThe ionization energy of sodium minus the electron affinity of chlorine, which way over here we said was 147 kilojoules per mole. So let me put that into joules so my units are consistent, 1.47 times ten to the fifth joules per mole. But now be careful here. When you calculate our star, this is for a molecule./nNot for a mole of molecules. I've got to change all of these things that are in here per mole to molecules, so I have got to multiply this by 6.022 times ten to the twenty-third molecules per mole. And then the value of r star is equal to 9.45 times ten to the minus ten meters./nThat is when the electron jumps. Let's draw a picture of what actually the relative size is here. So we have a sodium atom. That sodium atom has a diameter of about 3.8 angstroms. And we have a chlorine atom. That chlorine atom has a diameter of about two angstroms./nIt is 9.45 angstroms. That is the distance between those two neutral species, when that electron jump process actually happens. So they are pretty far apart, pretty far apart compared to the bond length of 2.36 angstroms./nAnd, indeed, it turns out that this number 9.45 angstroms is very, very close to what is measured experimentally when that electron jump process happens. This simple model treating sodium and chlorine as point charges works, but it works because sodium chloride is a very ionic bond. This simple model will not work for bonds that are not very ionic./nAll right? OK. See you Friday.
Tags //
Breakdown Octet Rule
Added: April 16, 2009, 10:56 pm
Runtime: 3010.27 | Views: 16306 |
Comments:0
Type: public Video
Status: Live!
Share this video with friends! Copy and paste the link above to an email or website.